《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

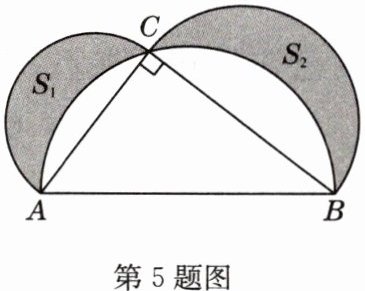
5 如图，阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形，已知S₁ + S₂ = 6，且AC + BC = 7，求AB的长.

答案： 解：由勾股定理，得$AC^{2}+BC^{2}=AB^{2}$。
∵$S_{1}+S_{2}=6$，
∴$\frac{1}{2}×\pi×(\frac{AC}{2})^{2}+\frac{1}{2}×\pi×(\frac{BC}{2})^{2}+\frac{1}{2}×AC×BC-\frac{1}{2}×\pi×(\frac{AB}{2})^{2}=6$，即$\frac{1}{2}AC·BC = 6$，
∴AC×BC = 12，
∴$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{(AC + BC)^{2}-2×AC×BC}=\sqrt{7^{2}-2×12}=\sqrt{25}=5$。

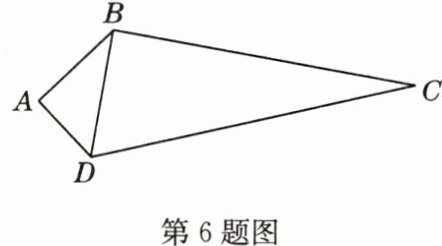
6 (经典题)如图，在四边形ABCD中，AB = 4，AD = 3，BC = 12，CD = x，x＞0，AB⊥AD.
(1)求BD的长.
(2)当x为何值时，△BDC为直角三角形?
(3)在(2)的条件下，求四边形ABCD的面积.

答案： 解：（1）
∵AB = 4，AD = 3，AB⊥AD，
∴$BD=\sqrt{AD^{2}+AB^{2}}=\sqrt{3^{2}+4^{2}} = 5$，即BD的长为5。 （2）在Rt△BCD中，BD = 5，BC = 12。 ①当CD为斜边时，由勾股定理知$CD=\sqrt{BD^{2}+BC^{2}}=\sqrt{5^{2}+12^{2}} = 13$。 ②当BC为斜边时，由勾股定理知$BC=\sqrt{BD^{2}+CD^{2}}$，即$12=\sqrt{5^{2}+CD^{2}}$，则$CD=\sqrt{119}$。 综上所述，当x为13或$\sqrt{119}$时，△BDC为直角三角形。 （3）①当CD为斜边时，$S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BCD}=\frac{1}{2}AB·AD+\frac{1}{2}BD·BC=\frac{1}{2}×4×3+\frac{1}{2}×5×12 = 36$。 ②当BC为斜边时，$S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BCD}=\frac{1}{2}AB·AD+\frac{1}{2}BD·CD=\frac{1}{2}×4×3+\frac{1}{2}×5×\sqrt{119}=6+\frac{5\sqrt{119}}{2}$。综上所述，四边形ABCD的面积是36或$6+\frac{5\sqrt{119}}{2}$。

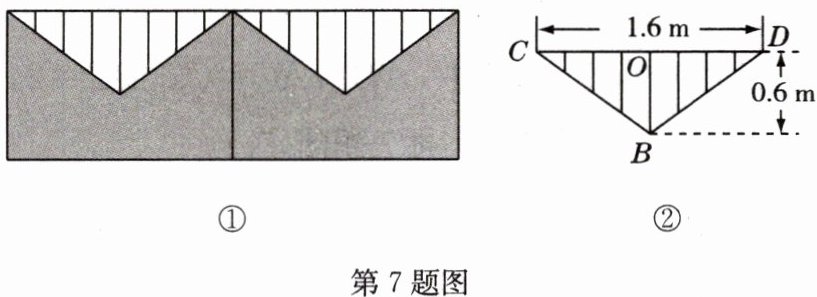
7 图①是围墙的一部分，上部分是由不锈钢管焊成的等腰三角形栅栏，如图②，请你根据图②所标注的尺寸，求焊成一个等腰三角形栅栏外框BCD至少需要不锈钢管多少米(焊接部分忽略不计).

答案： 解：由题意得BO⊥CD，
∵△BCD是等腰三角形，
∴$DO=\frac{1}{2}CD = 0.8$m。在Rt△BDO中，
∵$BD^{2}=DO^{2}+BO^{2}$，
∴$BD=\sqrt{0.8^{2}+0.6^{2}} = 1$（m），
∴BC = 1 m，
∴焊成一个等腰三角形栅栏外框BCD至少需要不锈钢管1 + 1 + 1.6 = 3.6（m）。

8 (实际应用题)小东和小明要测量校园里的一块四边形场地ABCD(如图所示)的周长，其中边CD上有水池及建筑遮挡，没有办法直接测量其长度.小东经测量得知AB = AD = 5 m，∠A = 60°，BC = 12 m，∠ABC = 150°.小明说根据小东所得的数据可以求出CD的长度.你同意小明的说法吗?若同意，请求出CD的长度；若不同意，请说明理由.

答案： 解：同意小明的说法。 连接BD。
∵AB = AD = 5 m，∠A = 60°，
∴△ABD是等边三角形，
∴BD = 5 m，∠ABD = 60°。
∵∠ABC = 150°，
∴∠DBC = 90°。
∴$DC=\sqrt{BC^{2}+BD^{2}}=\sqrt{12^{2}+5^{2}} = 13$（m）。
∴CD的长度为13 m。