《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1（2022·金华，中）如图是城市某区域的示意图，建立平面直角坐标系后，学校和体育场的坐标分别是(3,1)，(4, - 2)，下列各地点中，离原点最近的是（ ）


A. 超市
B. 医院
C. 体育场
D. 学校

答案： **A** 解析：根据学校和体育场的坐标建立平面直角坐标系， 超市到原点的距离为$\sqrt{2^{2}+1^{2}}=\sqrt{5}$， 医院到原点的距离为$\sqrt{3^{2}+1^{2}}=\sqrt{10}$， 学校到原点的距离为$\sqrt{3^{2}+1^{2}}=\sqrt{10}$， 体育场到原点的距离为$\sqrt{4^{2}+2^{2}}=2\sqrt{5}$。 故选 A。

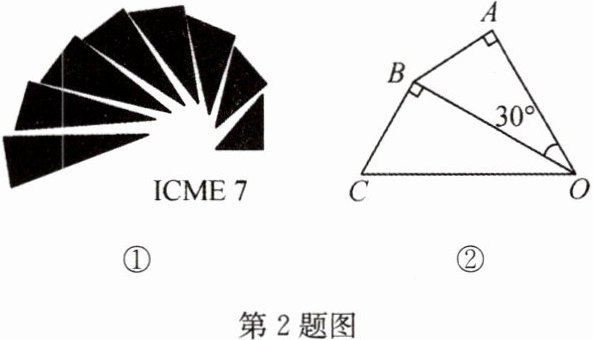
2（2022·遵义，中）如图①是第七届国际数学教育大会(ICME)会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图②所示的四边形OABC. 若AB = BC = 1，∠AOB = 30°，则点B到OC的距离为（ ）

A. $\frac{\sqrt{5}}{5}$
B. $\frac{2\sqrt{5}}{5}$
C. 1
D. 2

答案：
**B** 解析：作$BH\perp OC$于点$H$，
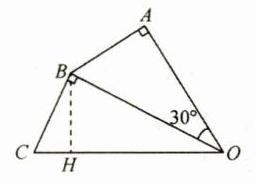
 $\because\angle AOB = 30^{\circ},\angle A = 90^{\circ},\therefore OB = 2AB = 2$， 在$Rt\triangle OBC$中，由勾股定理得， $OC=\sqrt{OB^{2}+BC^{2}}=\sqrt{2^{2}+1^{2}}=\sqrt{5}$， $\because S_{\triangle OBC}=\frac{1}{2}OB\cdot BC=\frac{1}{2}OC\cdot BH$， $\therefore BH=\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$。 故选 B。

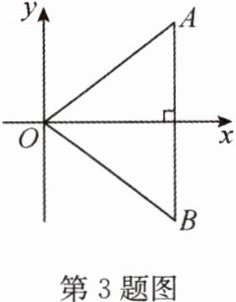
3（2022·天津，中）如图，△OAB的顶点O(0,0)，顶点A，B分别在第一、第四象限，且AB⊥x轴，若AB = 6，OA = OB = 5，则点A的坐标是（ ）

A. (5,4)
B. (3,4)
C. (5,3)
D. (4,3)

答案： **D** 解析：$\because AB\perp x$轴， $\therefore\angle ACO=\angle BCO = 90^{\circ}$，$\because OA = OB,OC = OC$， $\therefore\triangle ACO\cong\triangle BCO(HL)$， $\therefore AC = BC=\frac{1}{2}AB = 3$， $\because OA = 5$， $\therefore OC=\sqrt{5^{2}-3^{2}} = 4$， $\therefore$点$A$的坐标是$(4,3)$。故选 D。

4（2022·大庆，中）在平面直角坐标系中，点M在y轴的非负半轴上运动，点N在x轴上运动，满足OM + ON = 8. 点Q为线段MN的中点，则点Q的运动路径长为（ ）
A. 4π
B. 8$\sqrt{2}$
C. 8π
D. 16$\sqrt{2}$

答案： **B** 解析：设点$M$的坐标为$(0,m)$，点$N$的坐标为$(n,0)$，则点$Q$的坐标为$(\frac{n}{2},\frac{m}{2})$， $\because OM + ON = 8$， $\therefore|n|+m = 8(-8\leq n\leq8,0\leq m\leq8)$， 当$-8\leq n\lt0$时，$|n|+m=-n + m = 8$， $\therefore-\frac{n}{2}+\frac{m}{2}=4$，即$\frac{m}{2}=\frac{n}{2}+4$， $\therefore$此时点$Q$在一条线段上运动，线段的一个端点在$x$轴的负半轴上，坐标为$(-4,0)$，另一端点在$y$轴的正半轴上，坐标为$(0,4)$， $\therefore$此时点$Q$的运动路径长为$\sqrt{(-4)^{2}+4^{2}}=4\sqrt{2}$； 当$0\leq n\leq8$时，$|n|+m=n + m = 8$， $\therefore\frac{n}{2}+\frac{m}{2}=4$，即$\frac{m}{2}=4-\frac{n}{2}$， $\therefore$此时点$Q$在一条线段上运动，线段的一个端点在$x$轴的正半轴上，坐标为$(4,0)$，另一端点在$y$轴的正半轴上，坐标为$(0,4)$， $\therefore$此时点$Q$的运动路径长为$\sqrt{4^{2}+4^{2}}=4\sqrt{2}$。 综上可知，点$Q$的运动路径长为$4\sqrt{2}+4\sqrt{2}=8\sqrt{2}$。故选 B。

5（2022·齐齐哈尔，易）在△ABC中，AB = 3$\sqrt{6}$，AC = 6，∠B = 45°，则BC = ________.

答案： $3\sqrt{3}+3$或$3\sqrt{3}-3$ 解析：情况一：当$\triangle ABC$为锐角三角形时，如图①所示： 过$A$点作$AH\perp BC$于点$H$， $\because\angle B = 45^{\circ}$， $\therefore\triangle ABH$为等腰直角三角形， $\therefore AH = BH=\frac{AB}{\sqrt{2}}=\frac{3\sqrt{6}}{\sqrt{2}}=3\sqrt{3}$， 在$Rt\triangle ACH$中，由勾股定理可知：$CH=\sqrt{AC^{2}-AH^{2}}=\sqrt{36 - 27}=3$， $\therefore BC = BH + CH=3\sqrt{3}+3$。 情况二：当$\triangle ABC$为钝角三角形时，如图②所示。 由情况一知：$AH = BH=\frac{AB}{\sqrt{2}}=\frac{3\sqrt{6}}{\sqrt{2}}=3\sqrt{3}$，$CH=\sqrt{AC^{2}-AH^{2}}=\sqrt{36 - 27}=3$， $\therefore BC = BH - CH=3\sqrt{3}-3$。 故答案为$3\sqrt{3}+3$或$3\sqrt{3}-3$。

6（2022·金华，中）如图，在Rt△ABC中，∠ACB = 90°，∠A = 30°，BC = 2 cm. 把△ABC沿AB方向平移1 cm，得到△A'B'C'，连接CC'，则四边形AB'C'C的周长为________ cm.

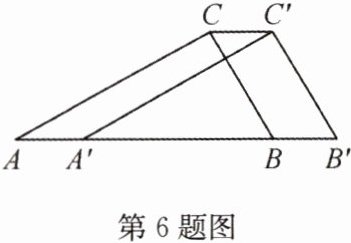
答案： $(8 + 2\sqrt{3})$ 解析：$\because\angle ACB = 90^{\circ},\angle A = 30^{\circ},BC = 2\ cm$， $\therefore AB = 2BC = 4\ cm$， $\therefore AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{16 - 4}=2\sqrt{3}(cm)$， $\because$把$\triangle ABC$沿$AB$方向平移$1\ cm$，得到$\triangle A'B'C'$， $\therefore CC' = 1\ cm,AB' = 4 + 1 = 5(cm),B'C' = BC = 2\ cm$， $\therefore$四边形$AB'C'C$的周长为$2\sqrt{3}+1 + 5 + 2=(8 + 2\sqrt{3})(cm)$， 故答案为$(8 + 2\sqrt{3})$。

7（2022·内江，难）勾股定理被记载于我国古代的数学著作《周髀算经》中，汉代数学家赵爽为了证明勾股定理，创制了一幅如图①所示的“弦图”，后人称之为“赵爽弦图”.图②由弦图变化得到，它是由八个全等的直角三角形拼接而成. 记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S₁、S₂、S₃.若正方形EFGH的边长为4，则S₁ + S₂ + S₃ = ________.

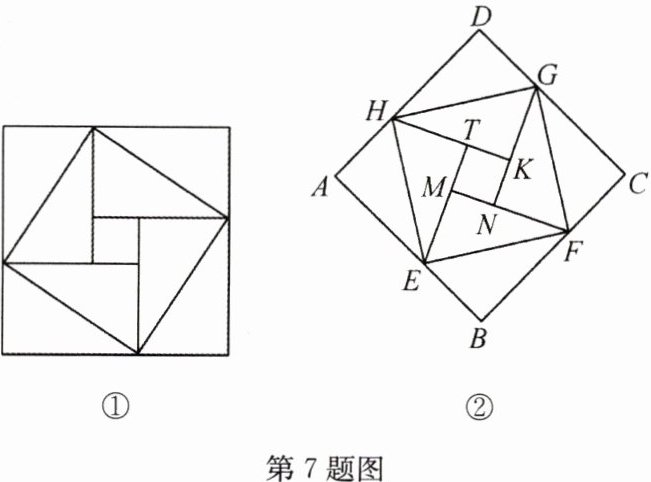
答案： $48$ 解析：设八个全等的直角三角形的长直角边长为$a$，短直角边长是$b$，则： $S_{1}=(a + b)^{2},S_{2}=4^{2}=16$， $S_{3}=(a - b)^{2}$。 又$a^{2}+b^{2}=EF^{2}=16$， $\therefore S_{1}+S_{2}+S_{3}=(a + b)^{2}+16+(a - b)^{2}$ $=2(a^{2}+b^{2})+16$ $=2\times16 + 16$ $=48$。 故答案为$48$。