《2025年1加1轻巧夺冠优化训练八年级数学下册人教版》

1 如图，一架等腰三角形形状的房梁，它的斜梁$AB = AC = 17$m，横梁$BC = 30$m，那么它的立柱$AD$的长度为（ ）

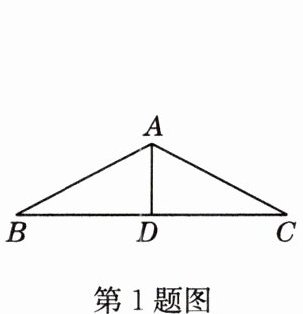
A. 6 m
B. 7 m
C. 8 m
D. 9 m

答案： C

2 如图，旗杆$AB$的顶端$A$垂下来的升旗使用的细绳$AC$比旗杆的高度多出4 m. 拉紧细绳的另一端点$C$按向地面，此时测得点$C$到旗杆底端$B$的距离为12 m，则旗杆$AB$的高度为（ ）

A. 12 m
B. 14 m
C. 16 m
D. 18 m

答案： C

3（2022·泰州）如图所示的象棋盘中，各个小正方形的边长均为1.“马”从图中的位置出发，不走重复路线，按照“马走日”的规则，走两步后的落点与出发点间的最短距离为______.

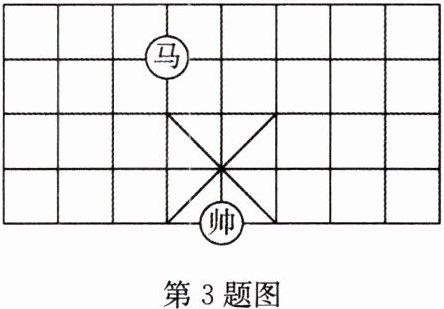
答案： $\sqrt{2}$

4 如图，在高为3 m，斜坡长为5 m的楼梯的表面铺地毯，至少需要地毯______m.

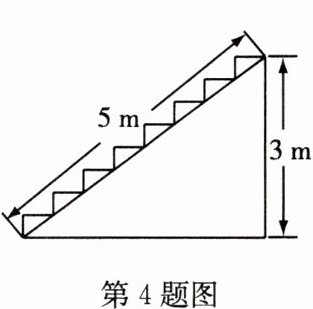
答案： 7

5 如图，某人欲横渡一条河，由于水流的作用，实际上岸地点$C$偏离到达点$B$ 50米，结果他在水中实际多游了10米，则该河的宽度为______米.

答案： 120 解析：设河宽$AB = x$米，则$AC=(x + 10)$米。由勾股定理，得$x^{2}+50^{2}=(x + 10)^{2}$，解得$x = 120$，$\therefore AB = 120$米。

6 如图，弧线为一段圆弧，在数轴上点$A$表示的实数是______.

答案： $-\sqrt{5}$

7 在数轴上画出表示$\sqrt{30}$的点（要求保留作图痕迹）.

答案：
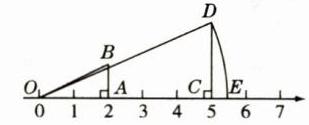
解：如图，作$\angle OAB = 90^{\circ}$，$OA = 2$，$AB = 1$，则$OB=\sqrt{1^{2}+2^{2}}=\sqrt{5}$，再作$\angle OCD = 90^{\circ}$，$OC = 5$，$DC = OB=\sqrt{5}$，则$OD=\sqrt{5^{2}+(\sqrt{5})^{2}}=\sqrt{30}$。以$O$为圆心，$OD$长为半径画弧交数轴于点$E$，则点$E$表示的数就是$\sqrt{30}$。

8（易错题）直线$l$的同侧有三个正方形$a,b,c$如图摆放，若$a,c$的面积分别是5和11，则$b$的面积为（ ）

A. 4
B. 6
C. 16
D. 25

答案：
C 解析：如图，易证$\triangle ABC\cong\triangle CED$，$\therefore AB = CE$。又$AB=\sqrt{5}$，$\therefore CE=\sqrt{5}$。又$DE=\sqrt{11}$，$\therefore CD^{2}=CE^{2}+DE^{2}=(\sqrt{5})^{2}+(\sqrt{11})^{2}=5 + 11 = 16$，$\therefore S_{b}=16$。

9 如图，有一块四边形模板$ABCD$，它的对角线$AC$与$BD$互相垂直，若$AB = 3$m，$BC = 4$m，$CD = 5$m，则$AD$的长为（ ）

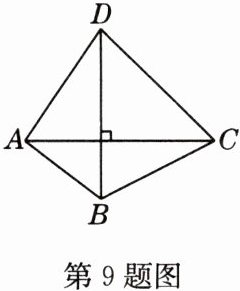
A. $3\sqrt{2}$m
B. 4 m
C. $2\sqrt{3}$m
D. $4\sqrt{2}$m

答案： A 解析：设$AC$与$BD$相交于点$O$，由勾股定理可得$AD^{2}=AO^{2}+DO^{2}=(AB^{2}-BO^{2})+(CD^{2}-CO^{2})=AB^{2}+CD^{2}-(BO^{2}+CO^{2})=AB^{2}+CD^{2}-BC^{2}=3^{2}+5^{2}-4^{2}=9 + 25 - 16 = 18$，$\therefore AD=\sqrt{18}=3\sqrt{2}$m。