《2025年顶尖课课练八年级数学下册华师大版》

10. 当$k$取不同的值时，$y$关于$x$的函数$y = kx + 1$（$k \neq 0$）的图象为总是经过点（0，1）的直线，我们把所有这样的直线合起来，称为经过点（0，1）的“直线束”，如图17.3.3 - 3所示. 则下面经过点（ - 1，1）的直线束的函数式是（ ）.
A. $y = kx - 1$（$k \neq 0$） B. $y = kx + k + 1$（$k \neq 0$） C. $y = kx - k + 1$（$k \neq 0$） D. $y = kx + k - 1$（$k \neq 0$）

答案： B

11. 如图17.3.3 - 4，已知两个受力面积分别为$S_A$（$m^2$）、$S_B$（$m^2$）（其中$S_A$、$S_B$为常数）的物体$A$、$B$，它们所受压强$p$（$Pa$）与压力$F$（$N$）的函数表达式是射线$l_A$、$l_B$，则$S_A$与$S_B$的大小关系是__________.

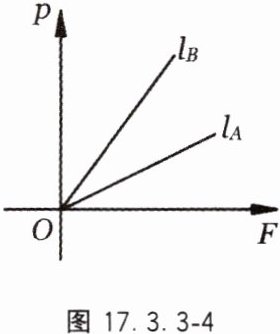
答案： Sₐ ＞ Sᵦ

12. 将直线$y = 2x$向右平移3个单位长度所得的直线的函数表达式是___________.

答案： y = 2x - 6

13. 关于自变量$x$的一次函数$y = mx - (m - 3)$的图象一定经过的定点是__________.

答案： (1, 3)

14. 某水果市场规定，凡购买不少于100 kg的某种水果，均按批发价结算. 小李携带现金3 000元到该市场采购橘子和苹果共1 000 kg进行零售，其批发价和零售价如下表所示：

设采购的苹果为$x$ kg，销售这两种水果所获得的总利润为$y$元.
（1）求$y$与$x$的函数表达式，并求出自变量$x$的取值范围；
（2）试画出(1)中所求函数的图象；
（3）求$y$的最大值.

答案： y = x + 1000（100 ≤ x ≤ 500）@@略@@1500元