《2025年通成学典课时作业本高中数学必修第二册人教版》

11. 如图，在四边形ABCD中，AC，BD相交于点O，$\boldsymbol{a} = \overrightarrow{DC}$，$\boldsymbol{b} = \overrightarrow{CO}$，$\boldsymbol{c} = \overrightarrow{OB}$，$\boldsymbol{d} = \overrightarrow{BA}$.

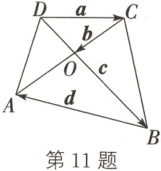
（1）$\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c} =$$\overrightarrow{DB}$；
（2）$\boldsymbol{b}+\boldsymbol{d}+\boldsymbol{c} =$$\overrightarrow{CA}$.

答案： 11.
(1)$\overrightarrow{DB}$
(2)$\overrightarrow{CA}$

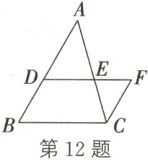
12. 如图，在$\triangle ABC$中，D，E分别是AB，AC上的点，F为线段DE延长线上一点，$DE// BC$，$AB// CF$，那么$\overrightarrow{AB}+\overrightarrow{DF} =$$\overrightarrow{AC}$；$\overrightarrow{AD}+\overrightarrow{FC} =$$\overrightarrow{AB}$.

答案： 12.$\overrightarrow{AC}$ $\overrightarrow{AB}$

13. 船在静水中的速度大小为20 m/min，水流的速度大小为10 m/min.若船从岸边出发沿垂直于水流的航线到达对岸，则经过1 h，该船的实际航程是多少千米？

答案：
13.解:如图，$\overrightarrow{AB}$表示水流的速度，$\overrightarrow{AC}$表示船实际航行的速度，$\overrightarrow{AD}$表示船在静水中航行的速度. 由题意可知，$|\overrightarrow{AD}| = 20 m/min$，$|\overrightarrow{AB}| = 10 m/min$，所以易得$\angle DAC = 30°$，即$|\overrightarrow{AC}| = 20 × \cos 30° = 10\sqrt{3} (m/min)$. 所以经过1 h，该船的实际航程是$10\sqrt{3} × 60 = 600\sqrt{3} (m)$，即$\frac {3\sqrt{3}} {5} km$.

14. 在某次抗震救灾中，一架飞机从A地按北偏东$35^{\circ}$的方向飞行800 km到达B地接到受伤人员，然后又从B地按南偏东$55^{\circ}$的方向飞行800 km将受伤人员送往C地医院，求这架飞机飞行的路程及两次位移的和.

答案：
14.解:如图. 依题意，得$|\overrightarrow{AB}| + |\overrightarrow{BC}| = 800 + 800 = 1600( km)$，$\alpha = 35°$，$\beta = 55°$，所以$\angle ABC = 35° + 55° = 90°$. 所以$|\overrightarrow{AC}| = \sqrt{|\overrightarrow{AB}|^2 + |\overrightarrow{BC}|^2} = \sqrt{800^2 + 800^2} = 800\sqrt{2}( km)$，且$\angle BAC = 45°$. 所以$\overrightarrow{AC}$的方向为北偏东$35° + 45° = 80°$. 所以这架飞机飞行的路程是$1600 km$，两次飞行的位移和为$\overrightarrow{AC}$，其大小为$800\sqrt{2} km$，方向为北偏东$80°$.