《2025年通成学典课时作业本高中数学必修第二册人教版》

10. (多选题)已知一个圆台的上、下底面半径分别为 10 和 20，它的侧面展开所得的扇环所对的圆心角为$180°$，则该圆台的 (ABD)

A.母线长为 20
B.表面积为$1 100\pi$
C.高为$10\sqrt{2}$
D.体积为$\frac{7 000\sqrt{3}\pi}{3}$

答案： 10.ABD

11. (2024·全国甲卷)已知甲、乙两个圆台上、下底面的半径均为$r_1$和$r_2$，母线长分别为$2(r_2 - r_1)$和$3(r_2 - r_1)$，则这两个圆台的体积之比$\frac{V_{甲}}{V_{乙}} =$$\frac{\sqrt{6}}{4}$ .

答案： 11.$\frac{\sqrt{6}}{4}$

12. (2025·黑龙江哈三中期中)如图，圆锥 PO 的底面直径和高均是 2，过 PO 的中点$O'$作平行于底面的截面，以该截面为底面挖去一个圆柱，则剩下的几何体的体积为 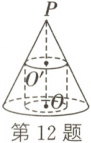$\frac{5π}{12}$ ，表面积为 $(\sqrt{5}+2)π$ .

答案： 12.$\frac{5π}{12}$，$(\sqrt{5}+2)π$

13. 已知水平放置的梯形 ABCO 按斜二测画法得到的直观图为梯形$A'B'C'O'$ (如图)，且$A'B' = 1$，$O'A' = 2$，$O'C' = 4$，现将梯形 ABCO 绕 OA 所在直线旋转一周得到一个几何体，求该几何体的侧面积.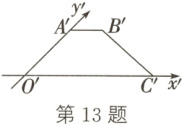

答案：
13.解:如图，根据题中直观图及斜二测画法，还原出水平放置的梯形ABCO。易知AO⊥OC，AB//OC，OC = OA = 4，AB = 1。所以将梯形ABCO绕OA所在直线旋转一周得到的几何体是圆台，且该圆台的上底面半径为1，下底面半径为4，母线长l = $\sqrt{4²+(4 - 1)²}$=5。所以该几何体的侧面积为S = π×(1 + 4)×5=25π。

14. 核心素养 数学建模 某养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪用).已建的仓库的底面直径为 12 m，高为 4 m.养路处拟建一个更大的圆锥形仓库，以存放更多食盐.现有两种方案：一是新建的仓库的底面直径比原来大 4 m(高不变)；二是新建的仓库的高度增加 4 m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积；
(2)分别计算按这两种方案所建的仓库的表面积；
(3)哪种方案更经济？
65

答案： 14.解:
(1)设两种方案所建的仓库的体积分别为V₁，V₂。方案一:仓库的底面直径变成12 + 4 = 16(m)，则V₁=$\frac{1}{3}$×π×($\frac{16}{2}$)²×4=$\frac{256}{3}$π(m³)；方案二:仓库的高变成4 + 4 = 8(m)，则V₂=$\frac{1}{3}$×π×($\frac{12}{2}$)²×8=96π(m³)。
(2)设两种方案所建的仓库的表面积分别为S₁，S₂。方案一:仓库的底面直径变成16m，即半径为8m，此时圆锥的母线长为$\sqrt{8²+4²}$=4$\sqrt{5}$(m)，则S₁=π×8×4$\sqrt{5}$+π×8²=(64π + 32$\sqrt{5}$π)m²；方案二:仓库的高变成8m，此时圆锥的母线长为$\sqrt{8²+6²}$=10(m)，则仓库的表面积S₂=π×6×(6 + 10)=96π(m²)。
(3)因为V₂＞V₁，S₂＜S₁，所以方案二比方案一更加经济。