《2025年练习生高中数学必修第二册人教B版》

7. 两千多年前我们的祖先就使用“算筹”表示数，后渐渐发展为算盘. 算筹有纵式和横式两种排列方式，0~9 各个数字及其算筹表示的对应关系如下表：

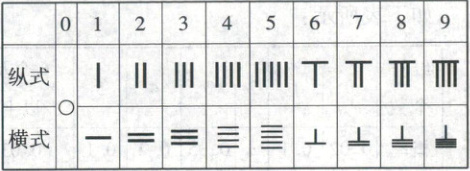
排列数字时，个位采用纵式，十位采用横式，百位采用纵式，千位采用横式……纵式和横式依次交替出现. 如表示 87，”表示 502. 在将按照一定顺序排列成无重复数字的三位数中任取一个，取到奇数的概率是(D)

A.0.7
B.0.6
C.0.4
D.0.3

答案： 7. D [解析]“$◯$”“$=$”“$\vert\vert\vert$”“$T$”“$=$”对应“0，2，3，6，9”，其中2与9要放在十位，3与6要放在个位或百位，0要放在个位或十位，所有情况列举如下：326，320，396，390，306，623，620，693，690，603，其中奇数有623，693，603。故取到奇数的概率是$\frac{3}{10} = 0.3$。选D。

8. [2021·山东青岛高一期末]在 E 区域 δ 病毒流行期间，为了让居民能及时了解疫情是否被控制，专家组通过会商一致认为：疫情被控制的指标是“连续 7 天每天新增感染人数不超过 5 人”，记连续 7 天每天记录的新增感染人数的数据为一个预报簇，根据最新的连续四个预报簇①②③④，依次计算得到结果如下：①平均数 $\overline{x} \leq 3$；②平均数 $\overline{x} \leq 3$，且标准差 $s \leq 2$；③平均数 $\overline{x} \leq 3$，且极差 $m \leq 2$；④众数等于 1，且极差 $m \leq 4$. 其中符合疫情被控制的指标的预报簇为(C)

A.①②
B.①③
C.③④
D.②④

答案： 8. C 破题关键：通过举反例说明预报簇不符合题意，根据平均数和标准差的统计意义，找出符合要求的选项即可。
[解析]①不符合，例如0，0，0，0，2，6，6，其平均数$\bar{x} = 2 \leq 3$，但有2天超过5人确诊，故不符合题意；②不符合，例如0，3，3，3，3，3，6，其平均数$\bar{x} \leq 3$且$s = \sqrt{\frac{18}{7}} \leq 2$，但有一天新增超过5人，故不符合题意；③符合，若7天中某一天新增感染人数$x$超过5人，即$x \geq 6$，则极差大于$6 - \bar{x}$，$6 - \bar{x} \geq 3$，所以假设不成立，故一定符合上述指标；④符合，若7天中某一天新增感染人数$x$超过5人，即$x \geq 6$，则极差不小于$6 - 1 = 5$，与极差小于或等于4相矛盾，所以假设不成立，故一定符合上述指标。选C。

9. [2022·甘肃天水高一期末]高一某班的同学在学习了“统计学初步”后，进行了交流讨论，甲同学说：“均值是刻画一组数据集中趋势最主要的指标.”乙同学说：“众数刻画了总体中个数的稳定或波动程度.”丙同学说：“方差越小，表明个体越整齐，波动越小.”丁同学说：“两组样本数据对比分析时，极差较大的一组数据其方差也较大.”其中说法正确的是(AC)

A.甲
B.乙
C.丙
D.丁

答案： 9. AC [解析]均值是刻画一组数据集中趋势最主要的指标，甲的说法正确。方差刻画了总体中个数的稳定或波动程度，乙的说法错误。方差越小，表明个体越整齐，波动越小，丙的说法正确。两组样本数据对比分析时，极差较大的一组数据不能说明其方差也较大，丁的说法错误。故选AC。

10. [2022·安徽宿州高一期末]下表记录了某地区一年之内的月降水量.

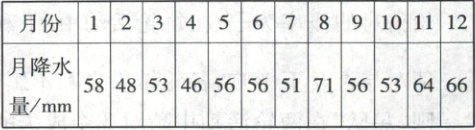
对于上述表格中的数据，说法正确的是(ACD)

A.该年份月降水量的极差是 25mm
B.该年份月降水量的众数是 53mm 和 56mm
C.该年份月降水量的 25%分位数是 52mm
D.该年份月降水量的中位数是 56mm

答案： 10. ACD [解析]该年份月降水量的极差是$71 - 46 = 25(mm)$，故A正确；该年份月降水量的众数是$56\ mm$，故B错误；该年份月降水量从小到大为46，48，51，53，53，56，56，56，58，64，66，71，$12 × 25\% = 3$，所以该年份月降水量的25%分位数是$\frac{51 + 53}{2} = 52(mm)$，故C正确；该年份月降水量从小到大为46，48，51，53，53，56，56，56，58，64，66，71，所以该年份月降水量的中位数是$\frac{56 + 56}{2} = 56(mm)$，故D正确。选ACD。

11. 下列说法中不正确的是(BCD)

A.若 A，B 为两个事件，则“A 与 B 互斥”是“A 与 B 相互对立”的必要不充分条件
B.若 A，B 为两个事件，则 $P(A \cup B) = P(A) + P(B)$
C.若事件 A，B，C 两两互斥，则 $P(A) + P(B) + P(C) = 1$
D.若事件 A，B 满足 $P(A) + P(B) = 1$，则 A 与 B 相互对立

答案： 11. BCD [解析]若$A,B$为两个事件，若“$A$与$B$互斥”，则“$A$与$B$不一定相互对立”；若“$A$与$B$相互对立”，则“$A$与$B$互斥”，则“$A$与$B$互斥”是“$A$与$B$相互对立”的必要不充分条件（对立事件是互斥事件的子集），所以选项A不符合题意。若$A,B$为两个事件，则$P(A \cup B) = P(A) + P(B) - P(A \cap B)$，所以选项B符合题意。若事件$A,B,C$两两互斥，则$P(A) + P(B) + P(C) = 1$不一定成立，如：掷骰子一次，记$A$为“向上的点数为1”，$B$为“向上的点数为2”，$C$为“向上的点数为3”，事件$A,B,C$两两互斥，则$P(A) + P(B) + P(C) = \frac{1}{6} + \frac{1}{6} + \frac{1}{6} = \frac{1}{2}$，所以选项C符合题意。袋中有除颜色外其余均相同的红球、黄球、黑球、绿球各1个，从袋中任意摸1个球，设事件$A$为“摸到红球或黄球”，事件$B$为“摸到黄球或黑球”，满足$P(A) + P(B) = 1$，但是$A$与$B$不对立，所以选项D符合题意。选BCD。

12. 下列说法中正确的为(BC)

A.在袋子中放有 2 白 2 黑大小相同的 4 个小球，甲、乙玩游戏的规则是从中不放回地依次随机摸出两个小球，如两球同色，则甲获胜，否则乙获胜，那么甲获胜的概率为 $\frac{2}{3}$
B.做 n 次随机试验，可以用事件 A 发生的频率估计事件 A 发生的概率
C.必然事件的概率为 1
D.在适宜的条件下种下一粒种子，观察它是否发芽，这个试验为古典概型

答案： 12. BC [解析]从4个小球中摸出两个小球共有6种方案，其中两个小球颜色相同的方案数为2，故甲获胜的概率为$\frac{1}{3}$，故A选项错误；随着试验次数的增加，频率会越来越接近概率，故可以用事件$A$发生的频率估计事件$A$发生的概率，故B选项正确；必然事件一定发生，故其概率是1，故C选项正确；古典概型要求随机事件的结果可能性相等，在适宜的条件下种下一粒种子，观察它是否发芽，这个试验发芽与不发芽可能性不一定相等，故D选项错误。故选BC。