《2025年练习生高中数学必修第二册人教B版》

1. [2018·全国卷Ⅲ改编]某公司有大量客户，且不同年龄段客户对其服务的评价有较大差异.为了了解客户的评价，该公司准备进行抽样调查，可供选择的抽样方法有简单随机抽样、分层随机抽样，则最合适的抽样方法是分层随机抽样.

答案： 1. 分层随机抽样
【解析】由于从不同年龄段客户中抽取，故采用分层随机抽样。

2. [2021·全国甲卷]为了解某地农村经济情况，对该地农户家庭年收入进行抽样调查，将农户家庭年收入的调查数据整理得到如下频率分布直方图：

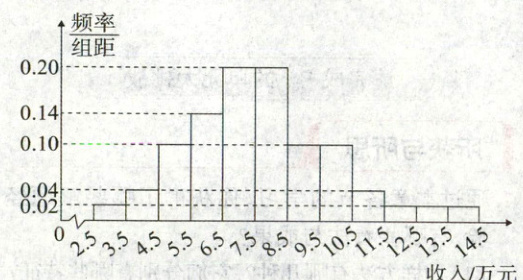
根据此频率分布直方图，下面结论中不正确的是(C)

A.该地农户家庭年收入低于 4.5 万元的农户比率估计为 6%
B.该地农户家庭年收入不低于 10.5 万元的农户比率估计为 10%
C.估计该地农户家庭年收入的平均值不超过 6.5 万元
D.估计该地有一半以上的农户，其家庭年收入介于 4.5 万元至 8.5 万元之间

答案： 2. C
破题关键 频率分布直方图中各矩形面积等于频率，样本频率直方图中的频率即可作为总体的相应比率的估计值。
【解析】该地农户家庭年收入低于$4.5$万元的农户的比率估计值为$(0.02 + 0.04)×1 = 0.06 = 6\%$，故A不符合题意；该地农户家庭年收入不低于$10.5$万元的农户比率估计值为$(0.04 + 0.02×3)×1 = 0.10 = 10\%$，故B不符合题意；该地农户家庭年收入介于$4.5$万元至$8.5$万元之间的比例估计值为$(0.10 + 0.14 + 0.20×2)×1 = 0.64 = 64\% ＞ 50\%$，故D不符合题意；该地农户家庭年收入的平均值的估计值为$3×0.02 + 4×0.04 + 5×0.10 + 6×0.14 + 7×0.20 + 8×0.20 + 9×0.10 + 10×0.10 + 11×0.04 + 12×0.02 + 13×0.02 + 14×0.02 = 7.68$（万元），超过$6.5$万元，故C符合题意。选C。

3. (多选)[2020·新高考Ⅱ卷]我国新冠肺炎疫情防控进入常态化，各地有序推进复工复产，下面是某地连续 11 天复工复产指数折线图，下列说法正确的是(CD)


A.这 11 天复工指数和复产指数均逐日增加
B.这 11 天期间，复产指数增量大于复工指数的增量
C.第 3 天至第 11 天复工复产指数均超过 80%
D.第 9 天至第 11 天复产指数增量大于复工指数的增量

答案： 3. CD
【解析】由题图可知，第1天到第2天复工指数减少，第7天到第8天复工指数减少，第10天到第11天复工指数减少，第8天到第9天复产指数减少，故A错误；由题图可知，第1天的复产指数与复工指数的差大于第11天的复产指数与复工指数的差，所以这11天期间，复产指数增量小于复工指数的增量，故B错误；由题图可知，第3天至第11天复工复产指数均超过$80\%$，故C正确；由题图可知，第9天至第11天复产指数增量大于复工指数的增量，故D正确。选CD。

4. [2022·全国甲卷]某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果，随机抽取 10 位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷，这 10 位社区居民在讲座前和讲座后问卷答题的正确率如下图：

则(B)

A.讲座前问卷答题的正确率的中位数小于 70%
B.讲座后问卷答题的正确率的平均数大于 85%
C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差

答案： 4. B
【解析】由统计图可知，讲座前这10位社区居民问卷答题的正确率分别为$65\%$，$60\%$，$70\%$，$60\%$，$65\%$，$75\%$，$90\%$，$85\%$，$80\%$，$95\%$。对于A项，将这10个数据从小到大排列为$60\%$，$60\%$，$65\%$，$65\%$，$70\%$，$75\%$，$80\%$，$85\%$，$90\%$，$95\%$，因此这10个数据的中位数是第5个与第6个数的平均数，为$\frac{70\% + 75\%}{2} = 72.5\% ＞ 70\%$，A错误。对于B项，由统计图可知，讲座后这10位社区居民问卷答题的正确率分别为$90\%$，$85\%$，$80\%$，$90\%$，$85\%$，$85\%$，$95\%$，$100\%$，$85\%$，$100\%$，所以讲座后这10位社区居民问卷答题的正确率的平均数为$\frac{1}{10}×(90\% + 85\% + 80\% + 90\% + 85\% + 85\% + 95\% + 100\% + 85\% + 100\%) = 89.5\% ＞ 85\%$，B正确。对于C项，讲座后这10位社区居民问卷答题的正确率的方差$s^{2}_{后} = \frac{1}{10}×[(90\% - 89.5\%)^{2} + (85\% - 89.5\%)^{2} + ·s + (85\% - 89.5\%)^{2} + (100\% - 89.5\%)^{2}] = \frac{42.25}{10000}$，所以标准差$s_{后} = 6.5\%$。讲座前这10位社区居民问卷答题的正确率的平均数为$\frac{1}{10}×(60\% + 60\% + 65\% + 65\% + 70\% + 75\% + 80\% + 85\% + 90\% + 95\%) = 74.5\%$，所以讲座前这10位社区居民问卷答题的正确率的方差为$s^{2}_{前} = \frac{1}{10}×[(60\% - 74.5\%)^{2} + (60\% - 74.5\%)^{2} + ·s + (90\% - 74.5\%)^{2} + (95\% - 74.5\%)^{2}] = \frac{142.25}{10000}$，所以标准差$s_{前} \approx 11.93\%$。所以$s_{前} ＞ s_{后}$，C错误。对于D项，讲座前问卷答题的正确率的极差为$95\% - 60\% = 35\%$，讲座后问卷答题的正确率的极差为$100\% - 80\% = 20\%$，D错误。故选B。
方法总结 本题以开展公益讲座普及垃圾分类知识为背景，引导学生关注实际生活，保护环境，树立环保意识，从我做起。以讲座前、后居民问卷答题的正确率为对比数据，考查中位数、平均数、标准差、极差等统计量，要求学生能够从图中读取数据，并利用数据说话，对学生的阅读理解能力、数据处理能力、分析问题和解决问题的能力要求比较高。