《2025年练习生高中数学必修第二册人教B版》

7. 一汽车厂生产 A,B,C 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表所示(单位:辆):

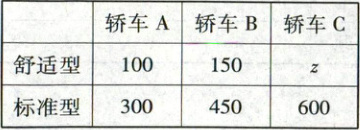
按类用分层随机抽样的方法在这个月生产的轿车中抽取 50 辆,其中有 A 类轿车 10 辆.
(1)求 z 的值;
(2)用分层随机抽样的方法在 C 类轿车中抽取一个容量为 5 的样本,应如何抽取?

答案： 7. 【解】
(1)设该厂本月生产轿车为n辆。依题意得$\frac{50}{n} = \frac{10}{100 + 300}$，解得$n = 2000$。
则$z = 2000 - 100 - 300 - 150 - 450 - 600 = 400$。
所以z的值是400。
(2)设所抽样本中有m辆舒适型轿车。
用分层随机抽样的方法在C类轿车中抽取一个容量为5的样本，则$\frac{400}{1000} = \frac{m}{5}$，解得$m = 2$。
所以在C类轿车中抽取2辆舒适型轿车，3辆标准型轿车。

8. 某中学举行体育运动会,同时进行全校精神文明擂台赛,为了了解这次活动在全校师生中产生的影响,分别对全校 500 名教职工、3 000 名初中生、4 000 名高中生进行问卷调查.
(1)如果要在所有问卷中抽出 120 份用于评估,请说明如何抽取才能得到比较客观的评估结论,并写出抽样过程.
(2)要从 3 000 份初中生的问卷中抽取一个容量为 48 的样本,如果采用简单随机抽样,应选什么方法?请说明理由.

答案： 8. 【解】
(1)由于总体容量较大，这次活动对教职工、初中生、高中生产生的影响差异较大，故采取分层随机抽样的方法进行抽样才能得到比较客观的评估结论。因为样本容量为120，总体容量为$500 + 3000 + 4000 = 7500$，则抽样比为$\frac{120}{7500} = \frac{2}{125}$，所以$500×\frac{2}{125} = 8$，$3000×\frac{2}{125} = 48$，$4000×\frac{2}{125} = 64$，所以在教职工、初中生、高中生中抽取的个体数分别是8，48，64。分层抽样的步骤如下：
①分层：分为教职工、初中生、高中生，共三层；
②确定每层抽取个体的个数：在教职工、初中生、高中生中抽取的个体数分别是8，48，64；
③各层分别按简单随机抽样的方法抽取样本；
④综合每层抽取的个体，组成样本。
这样便完成了整个抽样过程，就能得到比较客观的评估结论。
(2)简单随机抽样有两种方法：抽签法和随机数法。若用抽签法，则要做3000个号签，费时费力，因此应采用随机数法抽取样本。
方法总结 设计抽样方法时，应根据几种方法的适用范围来选择，并严格按照相应方法的步骤进行，同时需注意：
(1)采用抽签法的前提是制作号签方便，号签容易搅拌均匀；
(2)采用随机数法的关键是编号位数一致，读数时去掉重复的和不在编号范围内的号码；
(3)分层随机抽样应根据抽样比计算出各层应抽取的样本数，在进行层内抽样时，需明确采用的抽样方法，如抽签法、随机数法。

9. [2022·云南曲靖罗平第二中学高二期末]某居民区有 5 000 人自愿接种了抗病毒疫苗,其中 60~70 岁的老人有 1 400 人,16~18 岁的中学生有 400 人,其余为符合接种条件的其他年龄段的居民.在一项接种疫苗的追踪调查中,要用分层随机抽样的方法从该居民区 5 000 名接种疫苗的人群中抽取 50 人,则从其余符合接种条件的其他年龄段的居民中抽取的人数为32.

答案： 9. 32 【解析】由题意可得抽取60~70岁的老人和16~18岁的中学生为$\frac{1400 + 400}{5000}×50 = 18$（人），所以从其余符合接种条件的其他年龄段的居民中抽取的人数为$50 - 18 = 32$（人）。
易错规避 进行分层随机抽样的相关计算时，常利用以下关系式巧解：
(1)$\frac{样本容量n}{总体的个数N} = \frac{该层抽取的个体数}{该层的个体数}$；
(2)总体中某两层的个体数之比=样本中这两层抽取的个体数之比。

10. 我国古代数学名著《九章算术》中有如下问题，“今有北乡五千四百人，西乡四千四百八十人，南乡五千二百四十人，凡三乡，发役三百七十八人，欲以算数多少出之，何各几何？”意思是：北乡有 5 400 人，西乡有 4 480 人，南乡有 5 240 人，现要按人数多少从三乡共征集 378 人，问从各乡征集多少人？在上述问题中，需从西乡征集的人数是(B)

A.102
B.112
C.130
D.136

答案： 10. B 【解析】由题意可知，分层随机抽样的抽样比为$\frac{378}{5400 + 4480 + 5240} = \frac{1}{40}$，则需要从西乡征集的人数是$4480×\frac{1}{40} = 112$。故选B。
素养解读
素养 考查途径
数学运算 理解并会运用分层随机抽样的抽样比公式求得运算结果，考查数学运算的素养
逻辑推理 将古代数学问题转化成应用分层随机抽样问题，考查逻辑推理的素养