《2025年练习生高中数学必修第二册人教B版》

12. 有一种树木栽种五年后可成材, 在栽种后五年内, 年增长 $ 20\% $, 如果不砍伐, 从第六年到第十年, 年增长 $ 10\% $. 现有两种砍伐方案: 甲方案, 栽种五年后不砍伐, 等到十年后砍伐; 乙方案, 栽种五年后砍伐重栽, 再过五年再砍伐一次. 请计算后回答: 十年内哪个方案可以得到较多木材? (不考虑最初的树苗成本, 只按成材树木计算)

答案： 【解】设树木最初的栽种量为$a$。甲方案在十年后木材产量为$y_1 = a(1 + 20\%)^5(1 + 10\%)^5 = a(1.2 × 1.1)^5 \approx 4a$。乙方案在十年后木材产量为$y_2 = 2a(1 + 20\%)^5 = 2a × 1.2^5 \approx 4.98a$。因为$y_1 - y_2 = 4a - 4.98a = -0.98a ＜ 0$，所以十年内乙方案能获得更多的木材。

13. 在固定压力差 (压力差为常数) 下, 当气体通过圆形管道时, 其流量速度 $ R $ (单位: $ cm^3/s $) 与管道半径 $ r $ (单位: $ cm $) 的四次方成正比.
(1) 若气体在半径为 $ 3 cm $ 的管道中, 流量速度为 $ 400 cm^3/s $, 求该气体通过半径为 $ r $ (单位: $ cm $) 的管道时, 其流量速度 $ R $ (单位: $ cm^3/s $) 的函数解析式;
(2) 已知 (1) 中的气体通过的管道半径为 $ 5 cm $, 计算该气体的流量速度.

答案： 【解】
(1) 设$R = kr^4(k ＞ 0)$。因为$r = 3$，$R = 400$，所以$k = \frac{R}{r^4} = \frac{400}{81}$，故流量速度$R$的函数解析式为$R = \frac{400}{81}r^4$。
(2) 当$r = 5$时，该气体的流量速度$R = \frac{400}{81} × 5^4 = \frac{250000}{81} \approx 3086.4(cm^3/s)$。

14. 为了提高学生的学习效率, 某心理学研究小组在对学生上课注意力集中情况的调查研究中, 发现其注意力指数 $ p $ 与听课时间 $ t $ 之间的关系满足如图所示的曲线. 当 $ t \in (0,14] $ 时, 曲线是二次函数图像的一部分, 当 $ t \in (14,40] $ 时, 曲线是函数 $ y = 83 + \log_a(t - 5) $, $ a ＞ 0 $ 且 $ a \neq 1 $ 图像的一部分. 根据专家研究, 当注意力指数 $ p \geq 80 $ 时听课效果最佳.

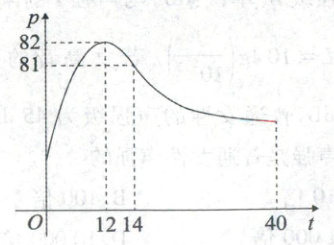
(1) 试求 $ p = f(t) $ 的函数关系式.
(2) 一道数学难题, 讲解需要 $ 22 $ 分钟, 问: 老师能否经过合理安排在学生听课效果最佳时讲解完? 请说明理由.

答案： 【解】
(1) 当$t \in (0, 14]$时，设$p = f(t) = c(t - 12)^2 + 82(c ＜ 0)$，将点$(14, 81)$的坐标代入，得$c = -\frac{1}{4}$，此时$p = f(t) = -\frac{1}{4}(t - 12)^2 + 82$，$t \in (0, 14]$；当$t \in (14, 40]$时，将点$(14, 81)$的坐标代入$y = \log_a(t - 5) + 83$，得$a = \frac{1}{3}$，此时$p = f(t) = \log_{\frac{1}{3}}(t - 5) + 83$，$t \in (14, 40]$。综上所述，$p = f(t) = \begin{cases} -\frac{1}{4}(t - 12)^2 + 82, & t \in (0, 14] \\ \log_{\frac{1}{3}}(t - 5) + 83, & t \in (14, 40] \end{cases}$。
(2) 当$t \in (0, 14]$时，令$-\frac{1}{4}(t - 12)^2 + 82 \geq 80$，解得$12 - 2\sqrt{2} \leq t \leq 12 + 2\sqrt{2}$，所以$t \in [12 - 2\sqrt{2}, 14]$；当$t \in (14, 40]$时，令$\log_{\frac{1}{3}}(t - 5) + 83 \geq 80$，解得$5 ＜ t \leq 32$，所以$t \in (14, 32]$。综上所述，当$t \in [12 - 2\sqrt{2}, 32]$时，学生听课效果最佳，此时$32 - (12 - 2\sqrt{2}) = 20 + 2\sqrt{2} ＞ 22$，教师能够合理安排时间讲完题目。