2025年练习生高中数学必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
18. [2022·安徽部分重点高中高一联考]幂函数 $ f(x) = (m^2 - m - 1)x^{m^2 + 2m - 5} $在区间 $ (0, +\infty) $上单调递增,且 $ a + b > 0 $,则 $ f(a) + f(b) $的值 (
A.恒大于 0
B.恒小于 0
C.等于 0
D.无法判断
A
)A.恒大于 0
B.恒小于 0
C.等于 0
D.无法判断
答案:
18. A[解析]由函数$f(x) = (m^2 - m - 1)x^m^2 + 2m - 5$是幂函数,得$m^2 - m - 1 = 1,$解得m = 2或m = −1。当m = 2时,$f(x) = x^3;$当m = −1时,f(x) = x^−6。因为函数f(x)在(0,+∞)上单调递增,所以$f(x) = x^3。$又a + b > 0,所以a > -b,所以f(a) > f(-b) = -f(b),所以f(a) + f(b) > 0。故选A。
19. [2022·湖北黄冈中学新兴分校高一期中]在同一平面直角坐标系内,函数 $ y = x^a (a \neq 0) $和 $ y = ax - \dfrac{1}{a} $的图像可能是 (
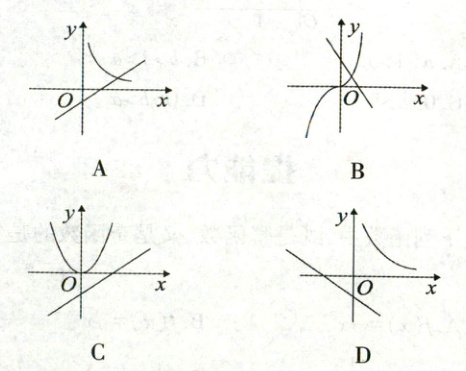
C
)
答案:
19. C 破题关键:结合直线与幂函数的图像的位置关系进行判断。
[解析]若a > 0,则函数y = x^a在(0,+∞)上单调递增,此时y = ax - $\frac{1}{a}$也单调递增;若a < 0,则函数y = x^a在(0,+∞)上单调递减,此时y = ax - $\frac{1}{a}$也单调递减。所以当x > 0时,y = x^a(a ≠ 0)和y = ax - $\frac{1}{a}$的单调性相同,所以排除A,B。选项D中,由y = x^a的图像可知a < 0,此时y = ax - $\frac{1}{a}$的图像与y轴的交点为(0,-$\frac{1}{a}$),该点在y轴正半轴上,所以排除D。故选C。
[解析]若a > 0,则函数y = x^a在(0,+∞)上单调递增,此时y = ax - $\frac{1}{a}$也单调递增;若a < 0,则函数y = x^a在(0,+∞)上单调递减,此时y = ax - $\frac{1}{a}$也单调递减。所以当x > 0时,y = x^a(a ≠ 0)和y = ax - $\frac{1}{a}$的单调性相同,所以排除A,B。选项D中,由y = x^a的图像可知a < 0,此时y = ax - $\frac{1}{a}$的图像与y轴的交点为(0,-$\frac{1}{a}$),该点在y轴正半轴上,所以排除D。故选C。
20. (多选)[2022·广东普宁高一期末]已知幂函数 $ y = f(x) $的图像经过点 $ (9,3) $,则下列结论正确的有 (
A.$ f(x) $为偶函数
B.$ f(x) $在定义域内为增函数
C.若 $ x > 1 $,则 $ f(x) > 1 $
D.若 $ x_2 > x_1 > 0 $,则 $ f \left( \dfrac{x_1 + x_2}{2} \right) > \dfrac{f(x_1) + f(x_2)}{2} $
BCD
)A.$ f(x) $为偶函数
B.$ f(x) $在定义域内为增函数
C.若 $ x > 1 $,则 $ f(x) > 1 $
D.若 $ x_2 > x_1 > 0 $,则 $ f \left( \dfrac{x_1 + x_2}{2} \right) > \dfrac{f(x_1) + f(x_2)}{2} $
答案:
20. BCD[解析]设f(x) = x^α。将点(9,3)的坐标代入,得3 = 9^α,则α = $\frac{1}{2}$,所以f(x) = x^$\frac{1}{2}$,所以f(x)的定义域为[0,+∞),所以f(x)不具有奇偶性,所以A不正确;因为$\frac{1}{2}$ > 0,所以函数f(x)在定义域[0,+∞)上为增函数,所以B正确;当x > 1时,$\sqrt{x}$ > 1,即f(x) > 1,所以C正确;若x_2 > x_1 > 0,则$(\frac{f(x_1) + f(x_2)}{2})^2 - [f(\frac{x_1 + x_2}{2})]^2 = (\frac{\sqrt{x_1} + \sqrt{x_2}}{2})^2 - (\sqrt{\frac{x_1 + x_2}{2}})^2 = \frac{x_1 + x_2 + 2\sqrt{x_1 x_2}}{4} - \frac{x_1 + x_2}{2} = \frac{2\sqrt{x_1 x_2} - x_1 - x_2}{4} = [f(\frac{x_1 + x_2}{2})]^2 - \frac{(\sqrt{x_1} - \sqrt{x_2})^2}{4} < 0$,即$\frac{f(x_1) + f(x_2)}{2} < f(\frac{x_1 + x_2}{2})$,所以D正确。故选BCD。
21. (多选)已知 $ \alpha \in \{ -1,1,2,3 \} $,则使函数 $ y = x^{\alpha} $的值域为 $ \mathbf{R} $,且为奇函数的 $ \alpha $的值为(
A.-1
B.1
C.2
D.3
BD
)A.-1
B.1
C.2
D.3
答案:
21. BD[解析]当α = -1时,y = x^−1 = $\frac{1}{x}$,为奇函数,但值域为{y|y ≠ 0},不满足条件;当α = 1时,y = x为奇函数,值域为R,满足条件;当α = 2时,y = x^2为偶函数,值域为{y|y ≥ 0},不满足条件;当α = 3时,y = x^3为奇函数,值域为R,满足条件。故选BD。
22. [2022·上海大同中学高一期中]已知幂函数 $ y = (m^2 + m - 1)x^{-5m - 3} $的图像过原点,则实数 $ m $的值为
−2
.
答案:
22. −2[解析]因为函数$y = (m^2 + m - 1)x^−5m - 3$是幂函数,所以$m^2 + m - 1 = 1,$解得m = -2或m = 1。当m = -2时,函数$y = x^7$的图像过原点,符合题意;当m = 1时,函数y = x^−8的图像不经过原点,不符合题意。综上可知,m = -2。
23. [2022·重庆巫山高一期末]若幂函数 $ f(x) $经过点 $ (2,8) $,则满足不等式 $ f(a - 3) + f(a - 1) \leqslant 0 $的实数 $ a $的取值范围是
(−∞,2]
.
答案:
23. (−∞,2][解析]不妨设f(x) = x^α。因为幂函数f(x)的图像过点(2,8),所以f
(2) = 2^α = 8,解得α = 3。所以$f(x) = x^3。$易知f(x)为定义在R上的奇函数,且f(x)为增函数。又f(a - 3) + f(a - 1) ≤ 0,所以f(a - 3) ≤ -f(a - 1) = f(1 - a),则a - 3 ≤ 1 - a,解得a ≤ 2。所以实数a的取值范围是(−∞,2]。
(2) = 2^α = 8,解得α = 3。所以$f(x) = x^3。$易知f(x)为定义在R上的奇函数,且f(x)为增函数。又f(a - 3) + f(a - 1) ≤ 0,所以f(a - 3) ≤ -f(a - 1) = f(1 - a),则a - 3 ≤ 1 - a,解得a ≤ 2。所以实数a的取值范围是(−∞,2]。
24. [2022·河北武安第一中学高一阶段考试]已知幂函数 $ f(x) = (m^2 - 2m + 2)x^{5k - 2k^2} (k \in \mathbf{Z}) $是偶函数,且在 $ (0, +\infty) $上单调递增.
(1)求函数 $ f(x) $的解析式;
(2)若 $ f(2x - 1) < f(2 - x) $,求实数 $ x $的取值范围.
(1)求函数 $ f(x) $的解析式;
(2)若 $ f(2x - 1) < f(2 - x) $,求实数 $ x $的取值范围.
答案:
24.[解]
(1)由题意知,m^2 - 2m + 2 = 1,解得m = 1。
易知5k - 2k^2 > 0[因为函数在(0,+∞)上单调递增],
所以0 < k < $\frac{5}{2}$(k ∈ Z),所以k = 1或k = 2。
当k = 1时,f(x) = x^3不是偶函数,舍去;
当k = 2时,f(x) = x^2是偶函数。
所以f(x) = x^2。
(2)因为函数f(x)为偶函数,
所以由f(2x - 1) < f(2 - x),得f(|2x - 1|) < f(|2 - x|),
所以|2x - 1| < |2 - x|,即(2x - 1)^2 < (2 - x)^2,即x^2 < 1,
所以x ∈ (−1,1)。
故实数x的取值范围为(−1,1)。
(1)由题意知,m^2 - 2m + 2 = 1,解得m = 1。
易知5k - 2k^2 > 0[因为函数在(0,+∞)上单调递增],
所以0 < k < $\frac{5}{2}$(k ∈ Z),所以k = 1或k = 2。
当k = 1时,f(x) = x^3不是偶函数,舍去;
当k = 2时,f(x) = x^2是偶函数。
所以f(x) = x^2。
(2)因为函数f(x)为偶函数,
所以由f(2x - 1) < f(2 - x),得f(|2x - 1|) < f(|2 - x|),
所以|2x - 1| < |2 - x|,即(2x - 1)^2 < (2 - x)^2,即x^2 < 1,
所以x ∈ (−1,1)。
故实数x的取值范围为(−1,1)。
25. [2022·湖南师大附中高一阶段考]已知幂函数 $ f(x) = (m^2 - 3m + 3)x^{m + 1} $的图像关于原点对称,则满足 $ (a + 1)^m > (3 - 2a)^m $成立的实数 $ a $的取值范围为
($\frac{2}{3}$,4)
.
答案:
25. ($\frac{2}{3}$,4)[解析]因为函数f(x) = (m^2 - 3m + 3)x^m + 1是幂函数,所以m^2 - 3m + 3 = 1,解得m = 1或m = 2。当m = 1时,f(x) = x^2是偶函数,其图像关于y轴对称,不符合题意;当m = 2时,f(x) = x^3是奇函数,其图像关于原点对称,符合题意,所以m = 2。所以不等式(a + 1)^m > (3 - 2a)^m可化为(a + 1)^2 > (3 - 2a)^2,即(3a - 2)(a - 4) < 0,解得$\frac{2}{3}$ < a < 4。所以实数a的取值范围为($\frac{2}{3}$,4)。
易错规避:根据幂函数的概念,确定参数m的取值,然后,需要针对参数m的取值情况进行分类讨论,找到符合题意的参数m的值。
易错规避:根据幂函数的概念,确定参数m的取值,然后,需要针对参数m的取值情况进行分类讨论,找到符合题意的参数m的值。
26. [2022·四川凉山高一期末]已知 $ a \neq 0 $,若 $ (a + b)^{2021} + a^{2021} + 2a + b = 0 $,则 $ \dfrac{b}{a} = $ (
A.-2
B.-1
C.$ -\dfrac{1}{2} $
D.2
A
)A.-2
B.-1
C.$ -\dfrac{1}{2} $
D.2
答案:
26. A[解析]设$\frac{b}{a}$ = k,则b = ak,所以由(a + b)^2021 + a^2021 + 2a + b = 0,得(a + ak)^2021 + a^2021 + 2a + ak = 0,即a^2021[(k + 1)^2021 + 1] + a(2 + k) = 0,亦即a^2020[(k + 1)^2021 + 1] + (2 + k) = 0。当(k + 1)^2021 + 1 = 0且2 + k = 0,即k = -2时,等式显然成立。当(k + 1)^2021 + 1 ≠ 0时,则有a^2020 = -$\frac{2 + k}{(k + 1)^2021 + 1}$。因为a ≠ 0,所以a^2020 = -$\frac{2 + k}{(k + 1)^2021 + 1}$ > 0。当2 + k < 0时,有(k + 1)^2021 + 1 > 0,即(k + 1)^2021 > (-1)^2021。因为函数y = x^2021是实数集上的增函数,所以由(k + 1)^2021 > (-1)^2021,得k + 1 > -1,则k + 2 > 0。这与2 + k < 0矛盾,所以(k + 1)^2021 + 1 > 0不成立。当2 + k > 0时,有(k + 1)^2021 + 1 < 0,即(k + 1)^2021 < (-1)^2021。因为函数y = x^2021是实数集上的增函数,所以由(k + 1)^2021 < (-1)^2021,得k + 1 < -1,则k + 2 < 0,这与2 + k > 0矛盾,所以(k + 1)^2021 + 1 < 0不成立。综上可知,k = -2。故选A。
27. [2022·湖北华中师大一附中高一期末]已知幂函数 $ y = x^a $的图像过点 $ \left( 3, \dfrac{1}{9} \right) $,则下列两个数的大小关系为 $ (x^2 - 2x + 4)^a $
≤
$ (-3)^a $.
答案:
27. ≤[解析]因为幂函数y = x^α的图像过点(3,$\frac{1}{9}$),所以3^α = $\frac{1}{9}$,解得α = -2。所以(x^2 - 2x + 4)^α - (-3)^α = $\frac{1}{(x^2 - 2x + 4)^2} - \frac{1}{9} = \frac{1}{[(x - 1)^2 + 3]^2} - \frac{1}{9}$。因为[(x - 1)^2 + 3]^2 ≥ 9,所以0 < $\frac{1}{[(x - 1)^2 + 3]^2}$ ≤ $\frac{1}{9}$,所以$\frac{1}{[(x - 1)^2 + 3]^2} - \frac{1}{9}$ ≤ 0,即(x^2 - 2x + 4)^α ≤ (-3)^α。
素养解读
| 素养 | 考查途径 |
| --- | --- |
| 数学运算 | 通过对幂函数的理解,掌握幂函数的性质,体现该素养 |
| 逻辑推理 | 通过幂函数的运算性质比较幂函数值的大小,体现该素养 |
| 数学运算 | 通过幂函数的图像特征求参数,体现该素养 |
| 逻辑推理 | 通过比较两个代数式的大小,体现该素养 |
素养解读
| 素养 | 考查途径 |
| --- | --- |
| 数学运算 | 通过对幂函数的理解,掌握幂函数的性质,体现该素养 |
| 逻辑推理 | 通过幂函数的运算性质比较幂函数值的大小,体现该素养 |
| 数学运算 | 通过幂函数的图像特征求参数,体现该素养 |
| 逻辑推理 | 通过比较两个代数式的大小,体现该素养 |
查看更多完整答案,请扫码查看


