《2025年练习生高中数学必修第二册人教B版》

21. [2020·全国卷Ⅰ]某厂接受了一项加工业务，加工出来的产品（单位：件）按标准分为 A，B，C，D 四个等级.加工业务约定：对于 A 级品、B 级品、C 级品，厂家每件分别收取加工费 90 元、50 元、20 元；对于 D 级品，厂家每件要赔偿原料损失费 50 元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为 25 元/件，乙分厂加工成本费为 20 元/件.厂家为决定由哪个分厂承接加工业务，在两个分厂各试加工了 100 件这种产品，并统计了这些产品的等级，整理如下：

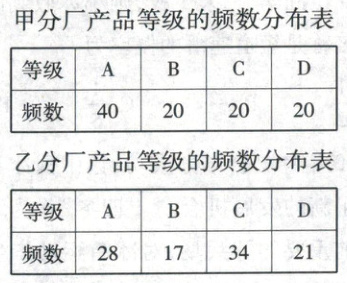
(1)分别估计甲、乙两分厂加工出来的一件产品为 A 级品的概率；
(2)分别求甲、乙两分厂加工出来的 100 件产品的平均利润，以平均利润为依据，厂家应选哪个分厂承接加工业务？

答案： 21. 【解】
(1) 由表可知，甲厂加工出来的一件产品为A级品的概率为$\frac{40}{100} = 0.4$，乙厂加工出来的一件产品为A级品的概率为$\frac{28}{100} = 0.28$。
(2) 甲分厂加工100件产品的总利润为$40×(90 - 25) + 20×(50 - 25) + 20×(20 - 25) - 20×(50 + 25) = 1500$（元），
所以甲分厂加工100件产品的平均利润为15元/件；
乙分厂加工100件产品的总利润为$28×(90 - 20) + 17×(50 - 20) + 34×(20 - 20) - 21×(50 + 20) = 1000$（元），
所以乙分厂加工100件产品的平均利润为10元/件。
故厂家应选择甲分厂承接加工任务。

22. [2020·全国卷Ⅰ]甲、乙、丙三位同学进行羽毛球比赛，约定赛制如下：累计负两场者被淘汰；比赛前抽签决定首先比赛的两人，另一人轮空；每场比赛的胜者与轮空者进行下一场比赛，负者下一场轮空，直至有一人被淘汰；当一人被淘汰后，剩余的两人继续比赛，直至其中一人被淘汰，另一人最终获胜，比赛结束.经抽签，甲、乙首先比赛，丙轮空.设每场比赛双方获胜的概率都为 $ \frac{1}{2} $，
(1)求甲连胜四场的概率；
(2)求需要进行第五场比赛的概率；
(3)求丙最终获胜的概率.

答案： 22. 【解】
(1) 记事件$M$为“甲连胜四场”，
则$P(M) = \left(\frac{1}{2}\right)^{4} = \frac{1}{16}$。
(2) 记事件$A$为“甲输”，事件$B$为“乙输”，事件$C$为“丙输”，
则四局内结束比赛的概率为$p' = P(ABAB) + P(ACAC) + P(BCBC) + P(BABA) = 4×\left(\frac{1}{2}\right)^{4} = \frac{1}{4}$，
所以需要进行第五场比赛的概率为$p = 1 - p' = \frac{3}{4}$。
(3) 记事件$A$为“甲输”，事件$B$为“乙输”，事件$C$为“丙输”，
记事件$M$为“甲赢”，事件$N$为“丙赢”，
则“甲赢”的基本事件包括：$BCBC$，$ABCBC$，$ACBCB$，$BABCC$，$BACBC$，$BCACB$，$BCABC$，$BCBAC$，
所以甲赢的概率为$P(M) = \left(\frac{1}{2}\right)^{4} + 7×\left(\frac{1}{2}\right)^{5} = \frac{9}{32}$。
由对称性可知，乙赢的概率和甲赢的概率相等，所以丙赢的概率为$P(N) = 1 - 2×\frac{9}{32} = \frac{7}{16}$。