《2025年练习生高中数学必修第二册人教B版》

1. [2022·上海复旦附中高二期末]已知事件 $ A,B,C $ 满足 $ A\subseteq B,B\subseteq C $，则下列说法不正确的是(D)

A.事件 $ A $ 发生一定导致事件 $ C $ 发生
B.事件 $ B $ 发生一定导致事件 $ C $ 发生
C.事件 $ \overline{A} $ 发生不一定导致事件 $ \overline{C} $ 发生
D.事件 $ \overline{C} $ 发生不一定导致事件 $ \overline{B} $ 发生

答案： 1.D 【解析】因为事件$A,B,C$满足$A\subseteq B,B\subseteq C$，所以$A\subseteq C$，所以$A$不符合题意；由$B\subseteq C$知事件$B$发生一定导致事件$C$发生，所以$B$不符合题意；因为$A\subseteq C$，所以$\overline{C}\subseteq \overline{A}$，所以事件$\overline{A}$发生不一定导致事件$\overline{C}$发生，所以$C$不符合题意；因为$B\subseteq C$，所以$\overline{C}\subseteq \overline{B}$，所以事件$\overline{C}$发生一定导致事件$\overline{B}$发生，所以$D$符合题意.故选$D$.

2. 从装有 2 个红球和 2 个白球的口袋内任取 2 个球，与事件“至少有 1 个白球”相等的事件是(C)

A.全是红球
B.至少有 1 个红球
C.至多有 1 个红球
D.1 个红球，1 个白球

答案： 2.C 【解析】从装有$2$个红球和$2$个白球的口袋内任取$2$个球，若至少有$1$个白球，则其包含的样本点是（白球，红球），（白球，白球）.又至多有$1$个红球包含的样本点也是（白球，红球），（白球，白球）.所以与事件“至少有$1$个白球”相等的事件是“至多有$1$个红球”.故选$C$.

3. 抛掷 3 枚质地均匀的硬币，记事件 $ A = \{ $ 至少 1 枚硬币正面朝上 $ \} $，事件 $ B = \{ $ 至多 2 枚硬币正面朝上 $ \} $，事件 $ C = \{ $ 没有硬币正面朝上 $ \} $，则(D)

A.$ C = A\cap B $
B.$ C = A\cup B $
C.$ C\subseteq A $
D.$ C\subseteq B $

答案： 3.D 【解析】记事件$D=\{1 枚硬币正面朝上\}$，$E=\{2 枚硬币正面朝上\}$，$F=\{3 枚硬币正面朝上\}$，则$A=D\cup E\cup F$，$B=C\cup D\cup E$，显然$C\neq A\cap B$，$C\neq A\cup B$，$C\subseteq B$，$C$不包含于$A$.故选$D$.

4. 抛掷一枚质地均匀的骰子，记事件 $ A = $“出现的点数是 1 或 2”，事件 $ B = $“出现的点数是 2 或 3 或 4”，则事件“出现的点数是 2”可以记为(B)

A.$ A\cup B $
B.$ A\cap B $
C.$ A\subseteq B $
D.$ A = B $

答案： 4.B 【解析】由题意，得$A=\{1,2\}$，$B=\{2,3,4\}$，$\therefore A\cup B=\{1,2,3,4\}$，$A\cap B=\{2\}$.故选$B$.

5. 事件 $ A,B $ 的概率分别为 $ p_1,p_2 $，且 $ p_1 ＜ p_2 $，则(D)

A.$ P(A\cap B) ＜ p_1 $
B.$ P(A\cup B) ＞ p_2 $
C.$ P(A\cup B) = p_2 + p_1 $
D.无法判断

答案： 5.D 【解析】因为不知道事件$A,B$的关系，所以无法判断.故选$D$.

6. [2022·河北保定高一期末]从装有两个红球和三个黑球的口袋里任取两个球，则互斥且不对立的两个事件是(A)

A.“都是红球”与“都是黑球”
B.“至少有一个红球”与“恰好有一个黑球”
C.“至少有一个红球”与“至少有一个黑球”
D.“都是红球”与“至少有一个黑球”

答案： 6.A 【解析】“都是红球”与“都是黑球”不可能同时发生，所以是互斥事件，但不是必然有一个发生，所以不是对立事件，故$A$符合题意；“至少有一个红球”与“恰好有一个黑球”不是互斥事件，故$B$不符合题意；“至少有一个红球”与“至少有一个黑球”不是互斥事件，故$C$不符合题意；“都是红球”与“至少有一个黑球”是互斥事件，也是对立事件，故$D$不符合题意.选$A$.

7. [2022·江苏徐州高一期末]同时抛掷两颗骰子，观察向上的点数，记事件 $ A = $“点数之和为 7”，事件 $ B = $“点数之和为 3 的倍数”，则(B)

A.$ A + B $ 为不可能事件
B.$ A $ 与 $ B $ 为互斥事件
C.$ AB $ 为必然事件
D.$ A $ 与 $ B $ 为对立事件

答案： 7.B 【解析】同时抛掷两颗骰子，有$36$个结果，事件$A=$“点数之和为$7$”，包括$(1,6)$，$(2,5)$，$(3,4)$，$(4,3)$，$(5,2)$，$(6,1)$.事件$B=$“点数之和为$3$的倍数”，包括$(1,2)$，$(2,1)$，$(1,5)$，$(5,1)$，$(2,4)$，$(4,2)$，$(3,3)$.所以$A+B$为“点数之和为$3$的倍数或为$7$”，不是不可能事件，故$A$错误；$A$与$B$为互斥事件，故$B$正确；$AB$为不可能事件，故$C$错误；事件$A,B$不能包含全部样本点，所以$A$与$B$不是对立事件，故$D$错误.选$B$.

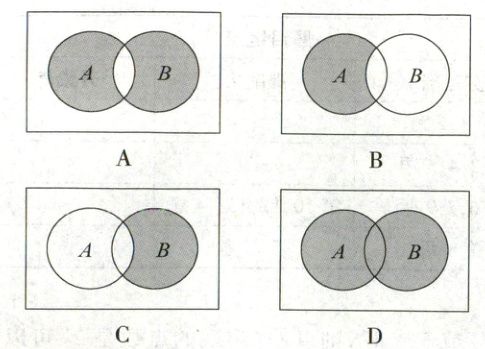
8. [2022·上海交大附中模拟预测]设 $ A,B $ 为随机事件，下列阴影部分能够表示 $ \overline{A}\cap B $ 的是(C)

答案： 8.C 【解析】$A$项中阴影部分表示$(A\cap \overline{B})\cup (\overline{A}\cap B)$，故$A$不符合题意；$B$项中阴影部分表示$A\cap \overline{B}$，故$B$不符合题意；$C$项中阴影部分表示$\overline{A}\cap B$，故$C$符合题意；$D$项中阴影部分表示$A\cup B$，故$D$不符合题意.选$C$.