《2025年练习生高中数学必修第二册人教B版》

4. [2022·云南玉溪第一中学高二期中]某校为了了解高二年级学生某次数学考试成绩的分布情况，从该年级的 1 120 名学生中随机抽取了 100 名学生的数学成绩，发现都在 $[80,150]$ 内. 现将这 100 名学生的成绩按照 $[80,90)$，$[90,100)$，$[100,110)$，$[110,120)$，$[120,130)$，$[130,140)$，$[140,150]$ 分组后，得到的频率分布直方图如图，则下列说法正确的是(C)


A.频率分布直方图中 $ a $ 的值为 0.040
B.样本数据中低于 130 分的频率为 0.3
C.总体的中位数(保留 1 位小数)估计为 123.3 分
D.总体分布在 $[90,100)$ 的频数一定与总体分布在 $[100,110)$ 的频数相等

答案： 4.C 【解析】由频率分布直方图得$(0.005 + 0.010 + 0.010 + 0.015 + a + 0.025 + 0.005)×10 = 1$（各矩形的面积和等于1），解得$a = 0.030$，故A错误；样本数据低于130分的频率为$1 - (0.025 + 0.005)×10 = 0.7$（要注意正难则反的原则），故B错误；$[80,120)$的频率为$(0.005 + 0.010 + 0.010 + 0.015)×10 = 0.4$，$[120,130)$的频率为$0.030×10 = 0.3$，所以总体的中位数（保留1位小数）估计为$120 + \frac{0.5 - 0.4}{0.3}×10\approx123.3$（分）（若中位数为$m$，则$x = m$把所有矩形分成面积相等的两部分），故C正确；样本分布在$[90,100)$的频数一定与样本分布在$[100,110)$的频数相等，总体分布在$[90,100)$的频数不一定与总体分布在$[100,110)$的频数相等，故D错误。选C。
易错规避 频率分布直方图中各矩形的面积和为1，满足某种条件的频率为对应矩形的面积和，若中位数为$m$，则$x = m$把所有矩形分成面积相等的两部分。

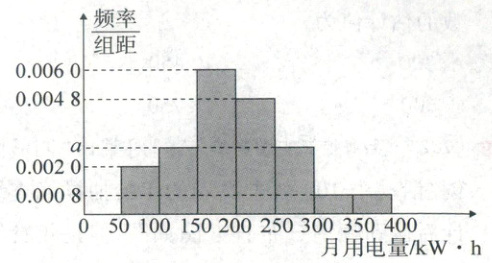
5. [2022·天津南开中学高三期中]某学校的环保志愿者小组为了研究 2 000 户家庭用电情况，在全校学生家庭中抽取了 100 户进行调查，发现这些家庭的月用电量都在 $ 50\sim 400\ kW·h $ 之间，并画出了如图的频率分布直方图. 则这 2 000 户家庭中，月用电量在 $ 250\sim 300\ kW·h $ 之间的户数为(D)


A.70
B.140
C.160
D.280

答案： 5.D 【解析】由频率分布直方图，得$(0.0020 + 2a + 0.0048 + 0.0060 + 2×0.0008)×50 = 1$，解得$a = 0.0028$，所以2 000户家庭中月用电量在250～300 kW·h之间的户数为$0.0028×50×2 000 = 280$。故选D。

6. 根据某校高三(1)班一次数学考试成绩整理得到如图的频率分布直方图，根据频率分布直方图估计该班学生的数学平均成绩为(B)


A.103
B.112.5
C.106.4
D.115

答案： 6.B 【解析】由频率分布直方图知，成绩由低到高的7个分组对应的频率依次为0.05，0.15，0.20，0.30，0.225，0.05，0.025，所以数学平均成绩为$85×0.05 + 95×0.15 + 105×0.2 + 115×0.3 + 125×0.225 + 135×0.05 + 145×0.025 = 112.5$，因而估计该班学生的数学平均成绩为112.5。故选B。

7. [2022·河南安阳高一期末]为了庆祝中国共产主义青年团成立 100 周年，某校甲、乙两个班共 70 人(甲班 40 人、乙班 30 人)参加了共产主义青年团知识竞赛，甲班的平均成绩为 77 分，方差为 123，乙班的平均成绩为 70 分，方差为 130，则甲、乙两班全部同学的成绩的方差为(C)

A.74
B.128
C.138
D.136

答案： 7.C 【解析】由总样本方差公式$s^{2}=\frac{1}{m + n}\left[ms_{1}^{2} + ns_{2}^{2} + \frac{mn}{m + n}(\bar{x}_{1} - \bar{x}_{2})^{2}\right]$，可得甲、乙两班全部同学的成绩的方差为$\frac{1}{40 + 30}\left[40×123 + 30×130 + \frac{40×30}{40 + 30}×(77 - 70)^{2}\right]=138$。故选C。

8. 2021 年起，某省将实行“3+1+2”高考模式，某中学为了了解本校学生的选考情况，随机调查了 100 名学生，其中选考化学或生物的学生共有 70 名，选考化学的学生共有 40 名，选考化学且选考生物的学生共有 20 名. 若该校共有 1 500 名学生，则该校选考生物的学生人数的估计值为(D)

A.300
B.450
C.600
D.750

答案： 8.D 【解析】因为选考化学或生物的学生共有70名，选考化学的学生共有40名，所以选考生物而没有选考化学的学生共有$70 - 40 = 30$（名）。又选考化学且选考生物的学生共有20名，所以选考生物的学生有$30 + 20 = 50$（名），所以在100名学生中选考生物的占比为$\frac{50}{100}$。又该校共有1 500名学生，则该校选考生物的学生人数的估计值为$\frac{50}{100}×1 500 = 750$。故选D。