《2025年练习生高中数学必修第二册人教B版》

13. [2022·黑龙江鸡西高一期中]函数 $f(x)=\log_{\frac{1}{3}}(x - x^{2})$ 的单调递减区间为(C)

A.$(-\infty,\frac{1}{2})$
B.$(\frac{1}{2},+\infty)$
C.$(0,\frac{1}{2})$
D.$(-\frac{1}{2},0)$

答案： 13. C [解析]令t=x−x²，则由t=x−x²＞0，得0＜x＜1。函数y=log₁/₃t是单调递减函数，要求f(x)=log₁/₃(x−x²)的单调递减区间，就要求t=x−x²的单调递增区间，而t=x−x²的单调递增区间为(−∞,$\frac{1}{2}$)，结合定义域，故f(x)=log₁/₃(x−x²)的单调递减区间为(0,$\frac{1}{2}$)。故选C。
易错规避 求对数型函数y=logₐf(x)（a＞0，a≠1）的单调区间，首先要注意确定函数的定义域，即必须使f(x)＞0有意义。

14. [2022·上海第三女子中学高一期末]设常数 $a ＞ 0$ 且 $a\neq1$，若函数 $y=\log_{a}(x + 1)$ 在区间 $[0,1]$ 上的最大值为 $1$，最小值为 $0$，则实数 $a$ 的值为2.

答案： 14. 2 [解析]令u=x+1，在[0,1]上单调递增。当0＜a＜1时，函数y=logₐu为减函数，所以函数y=logₐ(x+1)在区间[0,1]上单调递减。由题意可得$\begin{cases}f(0)=\log_{a}1=1,\\f(1)=\log_{a}2=0,\end{cases}$无解。当a＞1时，函数y=logₐu为增函数，所以函数y=logₐ(x+1)在区间[0,1]上单调递增。由题意可得$\begin{cases}f(0)=\log_{a}1=0,\\f(1)=\log_{a}2=1,\end{cases}$解得a=2。综上所述，a=2。
易错规避 当底数不是确定值，且底数的变化对求解结果有影响时，应分0＜a＜1与a＞1这两种情况讨论其单调性。

15. 函数 $y=\log_{3}x$，其中 $\frac{1}{3}\leq x\leq81$，则函数的值域为(C)

A.$(0,+\infty)$
B.$(\frac{1}{3},81)$
C.$[-1,4]$
D.$(1,4)$

答案： 15. C [解析]log₃$\frac{1}{3}$=log₃3⁻¹=−1，log₃81=log₃3⁴=4。因为y=log₃x在[$\frac{1}{3}$,81]上单调递增，所以y∈[−1,4]。故选C。

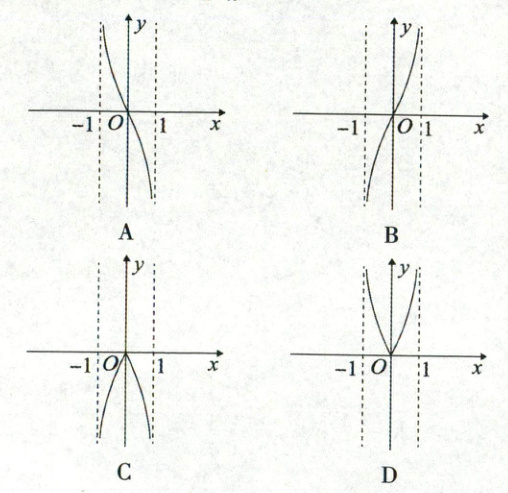
16. 函数 $f(x)=\log_{2}\frac{1 - x}{1 + x}$ 的图像大致为(A)

答案： 16. A [解析]由题意可知$\frac{1 - x}{1 + x}$＞0，即(x−1)(x+1)＜0，解得−1＜x＜1，所以函数f(x)的定义域为(−1,1)。因为f(−x)=log₂$\frac{1 + x}{1 - x}$=log₂($\frac{1 - x}{1 + x}$)⁻¹=−log₂$\frac{1 - x}{1 + x}$=−f(x)，所以f(x)为奇函数，图像关于原点对称，排除C,D选项。f($\frac{1}{2}$)=log₂$\frac{1 - \frac{1}{2}}{1 + \frac{1}{2}}$=log₂$\frac{1}{3}$＜0，排除B选项。故选A。

17. 函数 $y = f(x)$ 的图像如图所示，则 $f(x)$ 的解析式可能是(B)


A.$f(x)=(x + 1)\ln|x|$
B.$f(x)=(x - 1)\ln|x|$
C.$f(x)=x\ln|x|$
D.$f(x)=(x^{2}-1)\ln|x|$

答案： 17. B [解析]当x∈(0,1)时，x+1＞0，ln|x|＜0，所以f(x)=(x+1)ln|x|＜0，与题意不符，排除A；f(x)=xln|x|的定义域为(−∞,0)∪(0,+∞)，且f(−x)=−xln|-x|=−xln|x|=−f(x)，所以函数f(x)是奇函数，其图像关于原点对称，与题意不符，排除C；f(x)=(x²−1)ln|x|的定义域为(−∞,0)∪(0,+∞)，且f(−x)=[(−x)²−1]ln|-x|=(x²−1)ln|x|=f(x)，所以函数f(x)是偶函数，其图像关于y轴对称，与题意不符，排除D。故选B。

18. 若正实数 $a,b$ 满足 $\log_{2}a-\frac{1}{a + 1}=2\log_{4}b-\frac{1}{2b + 1}$，则(B)

A.$a ＞ 2b$
B.$a ＜ 2b$
C.$b ＞ 2a$
D.以上都不对

答案： 18. B [解析]由复合函数单调性知，f(x)=log₂x−$\frac{1}{x + 1}$在x∈(0,+∞)上单调递增。f(a)=log₂a−$\frac{1}{a + 1}$，f(2b)=log₂(2b)−$\frac{1}{2b + 1}$=2log₄b−$\frac{1}{2b + 1}$+1。因为log₂a−$\frac{1}{a + 1}$=2log₄b−$\frac{1}{2b + 1}$，所以f(a)=f(2b)−1，因此f(a)＜f(2b)，a＜2b。故选B。

19. [2022·山东潍坊高三期中]我们称可同时存在于一个指数函数与一个对数函数的图像上的点为“和谐点”，则四个点 $M(1,1),N(2,1),P(2,2),Q(2,-3)$ 中“和谐点”的个数为(A)

A.$1$
B.$2$
C.$3$
D.$4$

答案： 19. A [解析]设对数函数f(x)=logₐx，指数函数g(x)=bˣ，（a,b＞0且a,b≠1）。对于点M(1,1)，f
(1)=logₐ1=0，所以点M不在对数函数图像上，故点M不是“和谐点”。对于点N(2,1)，由f
(2)=logₐ2=1，解得a=2，即点N在对数函数f(x)=log₂x的图像上。又由g
(2)=b²=1，解得b=1，不符合题意，即点N不在指数函数图像上，故点N不是“和谐点”。对于点P(2,2)，由f
(2)=logₐ2=2，解得a=$\sqrt{2}$，即点P在对数函数f(x)=log₍√₂₎x的图像上。又由g
(2)=b²=2，解得b=$\sqrt{2}$，即点P在指数函数g(x)=($\sqrt{2}$)ˣ的图像上，故点P为“和谐点”。对于点Q(2,−3)，g
(2)=b²=−3，无解，故点Q不在指数函数图像上，故点Q不是“和谐点”。综上所述，四个点中，“和谐点”的个数为1。故选A。

20. [2022·上海延安中学高一期末]不等式 $\log_{4}x\leq\frac{1}{2}$ 的解集为(0,2].

答案： 20. (0,2] [解析]由题设可得log₄x≤log₄4^(1/2)[可根据对数函数的单调性转化为一般不等式(组)求解]，解得0＜x≤4^(1/2)=2，故不等式的解集为(0,2]。

21. 函数 $y = 2^{x}+\log_{a}(x + 1)+3$ 的图像恒过定点(0,4).

答案： 21. (0,4) [解析]
∵2⁰=1，logₐ1=0，
∴ 当x=0时，y=2⁰+logₐ(0+1)+3=1+0+3=4，
∴ 函数y=2ˣ+logₐ(x+1)+3的图像恒过定点(0,4)。

22. 函数 $f(x)=\log_{2}\frac{x}{4}×\log_{4}(4x^{2})$ 的最小值为-$\frac{9}{4}$.

答案： 22. -$\frac{9}{4}$ [解析]函数f(x)的定义域是(0,+∞)，log₂x∈R。
f(x)=log₂$\frac{x}{4}$×log₄(4x²)=(log₂x−2)(1+log₄x²)=(log₂x−2)(1+log₂x)=(log₂x)²−log₂x−2=(log₂x - $\frac{1}{2}$)² - $\frac{9}{4}$。所以当log₂x=$\frac{1}{2}$，即x=$\sqrt{2}$时，f(x)取得最小值 - $\frac{9}{4}$。