《2025年练习生高中数学必修第二册人教B版》

7. 甲、乙、丙三人参加一次考试,他们合格的概率分别为$\frac{2}{3}$,$\frac{3}{4}$,$\frac{2}{5}$,那么三人中恰有两人合格的概率是 (B)

A.$\frac{2}{5}$
B.$\frac{7}{15}$
C.$\frac{11}{30}$
D.$\frac{1}{6}$

答案： 7.B [解析]由题意知本题是一个相互独立事件同时发生的概率，三个人中恰有两个合格，包括三种情况，这三种情况是互斥的，所以三人中恰有两人合格的概率为$\frac{1}{3}×\frac{3}{4}×\frac{2}{5} + \frac{2}{3}×\frac{1}{4}×\frac{2}{5} + \frac{2}{3}×\frac{3}{4}×\frac{3}{5} = \frac{7}{15}$。故选B。

8. 某养鸡厂用鸡蛋孵化小鸡,用 200 个鸡蛋孵化出 170 只小鸡.由此估计,要孵化出 2500 只小鸡,大约需要鸡蛋的个数为(B)

A.3 022
B.2 941
C.2 800
D.3 125

答案： 8.B [解析]设大约需要$x$个鸡蛋，则$\frac{170}{200} = \frac{2500}{x}$，解得$x \approx 2941$。故选B。

9. 甲、乙两位同学玩游戏,对于给定的实数$a_1$,按下列方法操作一次产生一个新的实数:由甲、乙同时各掷一枚均匀的硬币,若出现两个正面朝上或两个反面朝上,则把$a_1$乘 2 后再减去 12;若出现一个正面朝上,一个反面朝上,则把$a_1$除以 2 后再加上 12,这样就得到一个新的实数$a_2$,对实数$a_2$仍按上述方法进行一次操作,又得到一个新的实数$a_3$,当$a_3 ＞ a_1$时,甲获胜,否则乙获胜.若甲获胜的概率为$\frac{3}{4}$,则$a_1$的取值范围是(-∞,12]∪[24,+∞).

答案： 9.$(-\infty,12]\cup[24,+\infty)$ [解析]$a_3$的结果有四种，每一个结果出现的概率都是$\frac{1}{4}$。
①$a_1 \to 2a_1 - 12 \to 2(2a_1 - 12) - 12 = 4a_1 - 36 = a_3$；
②$a_1 \to 2a_1 - 12 \to \frac{2a_1 - 12}{2} + 12 = a_1 + 6 = a_3$；
③$a_1 \to \frac{a_1}{2} + 12 \to \frac{\frac{a_1}{2} + 12}{2} + 12 = \frac{a_1}{4} + 18 = a_3$；
④$a_1 \to \frac{a_1}{2} + 12 \to 2\left(\frac{a_1}{2} + 12\right) - 12 = a_1 + 12 = a_3$。
$\because a_1 + 6 ＞ a_1$，$a_1 + 12 ＞ a_1$，$\therefore$要使甲获胜的概率为$\frac{3}{4}$，即$a_3 ＞ a_1$的概率为$\frac{3}{4}$，$\therefore 4a_1 - 36 ＞ a_1$，$\frac{a_1}{4} + 18 \leq a_1$，或$4a_1 - 36 \leq a_1$，$\frac{a_1}{4} + 18 ＞ a_1$，解得$a_1 \leq 12$或$a_1 \geq 24$。

10. [2022·辽宁沈阳高三模拟]流行性感冒多由病毒引起,据调查,空气相对湿度过大或过小时,都有利于一些病毒的繁殖和传播.科学测定,当空气相对湿度大于 65%或小于 40%时,病毒繁殖滋生较快,当空气相对湿度在 45%~55%时,病毒死亡较快.现随机抽取了全国部分城市,获得了它们的空气月平均相对湿度共 300 个数据,整理得到数据分组及频数分布表,其中为了记录方便,将空气相对湿度在$a\%$~$b\%$时记为区间$[a,b)$.
(1)求上述数据中空气相对湿度使病毒死亡较快的频率;
(2)从区间$[15,35)$的数据中任取两个数据,求恰有一个数据位于$[25,35)$内的概率;
(3)假设同一组中的每个数据都可以用该组区间的中点值代替,

试

估计样本中空气月平均相对湿度的平均数在第几组.

答案： 10.[解]
(1)当空气相对湿度在$45\% \sim 55\%$时，病毒死亡较快，
而样本在$[45,55)$上的频数为30，
所以所求频率为$p = \frac{30}{300} = \frac{1}{10}$。
(2)设事件$A$为“从区间$[15,35)$的数据中任取两个数据，恰有一个数据位于$[25,35)$内”。
设区间$[15,25)$中的两个数据为$a_1,a_2$，区间$[25,35)$中的三个数据为$b_1,b_2,b_3$。
从区间$[15,35)$的数据中任取两个数据，
包含的样本空间为$\varOmega = \{(a_1,a_2),(a_1,b_1),(a_1,b_2),(a_1,b_3),(a_2,b_1),(a_2,b_2),(a_2,b_3),(b_1,b_2),(b_1,b_3),(b_2,b_3)\}$，共10个样本点，
而事件$A = \{(a_1,b_1),(a_1,b_2),(a_1,b_3),(a_2,b_1),(a_2,b_2),(a_2,b_3)\}$，共6个样本点，所以$P(A) = \frac{6}{10} = \frac{3}{5}$。
(3)样本的平均数为$\overline{x} = \frac{20×2 + 30×3 + 40×15 + 50×30 + 60×50 + 70×75 + 80×120 + 90×5}{300} \approx 68.43$，
故样本中空气月平均相对湿度的平均数在第6组。

11. [2022·河南信阳高一月考]已知$n$是一个三位正整数,若$n$的个位数字大于十位数字,十位数字大于百位数字,则称$n$为“三位递增数”(如 135,256,345 等).现要从甲、乙两名同学中选出一人参加某市组织的数学竞赛,选取的规则如下:从由 1,2,3,4,5,6 组成的所有“三位递增数”中随机抽取 1 个数,若抽取的“三位递增数”是偶数,则甲参加数学竞赛;若抽取的“三位递增数”是奇数,则乙参加数学竞赛.
(1)由 1,2,3,4,5,6 可组成多少个“三位递增数”? 分别用树状图法和列举法解答.
(2)这种选取规则对甲、乙两名同学公平吗?请说明理由.

答案：
11.[解]
(1)树状图法：画出树状图，如图所示。

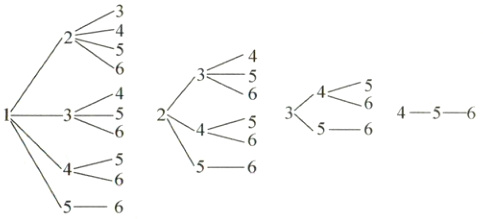
从上面的树状图可知，由1,2,3,4,5,6可组成20个“三位递增数”。
列举法：由1,2,3,4,5,6组成的“三位递增数”分别是123,124,125,126,134,135,136,145,146,156,234,235,236,245,246,256,345,346,356,456，共20个，
故由1,2,3,4,5,6可组成20个“三位递增数”。
(2)不公平。
由
(1)知由1,2,3,4,5,6组成的“三位递增数”有20个。
记“甲参加数学竞赛”为事件$A$，事件$A$包含的样本点有124,126,134,136,146,156,234,236,246,256,346,356,456，共13个，
所以$P(A) = \frac{13}{20}$。
记“乙参加数学竞赛”为事件$B$，则事件$B$包含的样本点有123,125,135,145,235,245,345，共7个，
所以$P(B) = \frac{7}{20}$。
因为$P(A) ＞ P(B)$，所以该选取规则对甲、乙两名同学不公平。