2025年练习生高中数学必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
10. [2022·江苏南京六校高一联考]设$a=\log_{3}6$,$b=\log_{2}\frac{1}{6}$,则下列结论正确的有(
A.$\frac{1}{a}-\frac{1}{b}=1$
B.$\frac{1}{a}+\frac{1}{b}=1$
C.$a + b < 0$
D.$\frac{1}{a^{2}}-\frac{1}{b^{2}} < 0$
AC
)A.$\frac{1}{a}-\frac{1}{b}=1$
B.$\frac{1}{a}+\frac{1}{b}=1$
C.$a + b < 0$
D.$\frac{1}{a^{2}}-\frac{1}{b^{2}} < 0$
答案:
10. AC 【解析】因为$\frac{1}{a}-\frac{1}{b}=\log_{6}3+\log_{6}2 = 1$,所以A正确。因为$\frac{1}{a}+\frac{1}{b}=\log_{6}3-\log_{6}2=\log_{6}\frac{3}{2}\neq1$,所以B错误。因为$\frac{1}{a}+\frac{1}{b}=\log_{6}\frac{3}{2}\gt0$,所以$\frac{a + b}{ab}\gt0$。而$ab\lt0$,所以$a + b\lt0$,所以C正确。因为$\frac{1}{a^{2}}-\frac{1}{b^{2}}=\left(\frac{1}{a}-\frac{1}{b}\right)\left(\frac{1}{a}+\frac{1}{b}\right)=\frac{1}{a}+\frac{1}{b}\gt0$,所以D错误,故选AC。
11. 如图是某受污染的湖泊在自然净化过程中某种有害物质的剩留量$y$与净化时间$t$(月)的近似函数关系:$y = a^{t}(a > 0,a\neq1,t\geq0)$的图像. 以下说法正确的有(
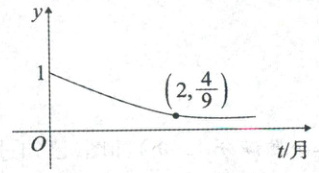
A.每月减少的有害物质质量都相等
B.第 4 个月时,剩留量就会低于$\frac{1}{5}$
C.污染物每月的衰减率为$\frac{1}{3}$
D.当剩留$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$时,所经过的时间分别是$t_{1}$,$t_{2}$,$t_{3}$,则$t_{1}+t_{2} > t_{3}$
BC
)
A.每月减少的有害物质质量都相等
B.第 4 个月时,剩留量就会低于$\frac{1}{5}$
C.污染物每月的衰减率为$\frac{1}{3}$
D.当剩留$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$时,所经过的时间分别是$t_{1}$,$t_{2}$,$t_{3}$,则$t_{1}+t_{2} > t_{3}$
答案:
11. BC 【解析】$\because y = a^{t}(a\gt0$且$a\neq1$,$t\geq0)$的图像经过点$\left(2,\frac{4}{9}\right)$,$\therefore\frac{4}{9}=a^{2}$,$\therefore a=\frac{2}{3}$,即$y=\left(\frac{2}{3}\right)^{t}$。1月到2月,减少的有害物质质量为$\frac{2}{3}-\frac{4}{9}=\frac{2}{9}$,2月到3月,减少的有害物质质量为$\frac{4}{9}-\frac{8}{27}=\frac{4}{27}$,故每月减少的有害物质质量都相等是错误的,故A错误;当$t = 4$时,有害物质的剩留量$y=\frac{16}{81}\lt\frac{1}{5}$,故B正确;污染物每月的衰减率为$1-\frac{2}{3}=\frac{1}{3}$,故C正确;当剩留$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$时,所经过的时间分别是$t_{1}$,$t_{2}$,$t_{3}$,则$\left(\frac{2}{3}\right)^{t_{1}}=\frac{1}{2}$,$\left(\frac{2}{3}\right)^{t_{2}}=\frac{1}{4}$,$\left(\frac{2}{3}\right)^{t_{3}}=\frac{1}{8}$,则$t_{1}=\log_{\frac{2}{3}}\frac{1}{2}$,$t_{2}=\log_{\frac{2}{3}}\frac{1}{4}$,$t_{3}=\log_{\frac{2}{3}}\frac{1}{8}$,则$t_{1}+t_{2}=t_{3}$,故D错误。选BC。
12. [2022·河北保定高一期末]若$f(x)=x+\frac{1}{x}$,$g(x)=\lg x + 2$,则(
A.函数$f(x)$为奇函数
B.当$x_{1},x_{2}\in(0,+\infty)$时,$\frac{f(x_{1})+f(x_{2})}{2}\leq f(\frac{x_{1}+x_{2}}{2})$
C.当$x_{1},x_{2}\in(0,+\infty)$时,$\frac{g(x_{1})+g(x_{2})}{2}\leq g(\frac{x_{1}+x_{2}}{2})$
D.函数$h(x)=f(x)-g(x)$有两个零点
ACD
)A.函数$f(x)$为奇函数
B.当$x_{1},x_{2}\in(0,+\infty)$时,$\frac{f(x_{1})+f(x_{2})}{2}\leq f(\frac{x_{1}+x_{2}}{2})$
C.当$x_{1},x_{2}\in(0,+\infty)$时,$\frac{g(x_{1})+g(x_{2})}{2}\leq g(\frac{x_{1}+x_{2}}{2})$
D.函数$h(x)=f(x)-g(x)$有两个零点
答案:
12. ACD 【解析】函数$f(x)=x+\frac{1}{x}$的定义域为$\{x\mid x\neq0\}$,因为$f(-x)=-x-\frac{1}{x}=-f(x)$,所以函数$f(x)=x+\frac{1}{x}$为奇函数,故A正确。因为$\frac{f(x_{1})+f(x_{2})}{2}-f\left(\frac{x_{1}+x_{2}}{2}\right)=\frac{\left(x_{1}+\frac{1}{x_{1}}\right)+\left(x_{2}+\frac{1}{x_{2}}\right)}{2}-\left(\frac{x_{1}+x_{2}}{2}+\frac{2}{x_{1}+x_{2}}\right)=\frac{1}{2}\left(\frac{1}{x_{1}}+\frac{1}{x_{2}}\right)-\frac{2}{x_{1}+x_{2}}=\frac{x_{1}+x_{2}}{2x_{1}x_{2}}-\frac{2}{x_{1}+x_{2}}=\frac{(x_{1}+x_{2})^{2}-4x_{1}x_{2}}{2x_{1}x_{2}(x_{1}+x_{2})}=\frac{(x_{1}-x_{2})^{2}}{2x_{1}x_{2}(x_{1}+x_{2})}\geq0$,当且仅当$x_{1}=x_{2}$时取等号,所以$\frac{f(x_{1})+f(x_{2})}{2}\geq f\left(\frac{x_{1}+x_{2}}{2}\right)$,故B错误。因为$g\left(\frac{x_{1}+x_{2}}{2}\right)-\frac{g(x_{1})+g(x_{2})}{2}=\lg\frac{x_{1}+x_{2}}{2}+2-\frac{(\lg x_{1}+2)+(\lg x_{2}+2)}{2}=\lg\frac{x_{1}+x_{2}}{2}-\frac{1}{2}\lg(x_{1}x_{2})=\lg\frac{x_{1}+x_{2}}{2\sqrt{x_{1}x_{2}}}\geq\lg\frac{2\sqrt{x_{1}x_{2}}}{2\sqrt{x_{1}x_{2}}}=0$,当且仅当$x_{1}=x_{2}$时取等号,所以$g\left(\frac{x_{1}+x_{2}}{2}\right)\geq\frac{g(x_{1})+g(x_{2})}{2}$,故C正确。令$h(x)=0$,则有$f(x)=g(x)$,函数$h(x)=f(x)-g(x)$的零点即为函数$f(x)$与函数$g(x)$图像交点的横坐标。在同一平面直角坐标系中,分别画出$f(x)=x+\frac{1}{x}(x\gt0)$和$g(x)=\lg x + 2$的图像,如图所示。
根据函数$f(x)$和$g(x)$的图像可知,函数$h(x)$有且仅有两个零点,故D正确。
选ACD。

12. ACD 【解析】函数$f(x)=x+\frac{1}{x}$的定义域为$\{x\mid x\neq0\}$,因为$f(-x)=-x-\frac{1}{x}=-f(x)$,所以函数$f(x)=x+\frac{1}{x}$为奇函数,故A正确。因为$\frac{f(x_{1})+f(x_{2})}{2}-f\left(\frac{x_{1}+x_{2}}{2}\right)=\frac{\left(x_{1}+\frac{1}{x_{1}}\right)+\left(x_{2}+\frac{1}{x_{2}}\right)}{2}-\left(\frac{x_{1}+x_{2}}{2}+\frac{2}{x_{1}+x_{2}}\right)=\frac{1}{2}\left(\frac{1}{x_{1}}+\frac{1}{x_{2}}\right)-\frac{2}{x_{1}+x_{2}}=\frac{x_{1}+x_{2}}{2x_{1}x_{2}}-\frac{2}{x_{1}+x_{2}}=\frac{(x_{1}+x_{2})^{2}-4x_{1}x_{2}}{2x_{1}x_{2}(x_{1}+x_{2})}=\frac{(x_{1}-x_{2})^{2}}{2x_{1}x_{2}(x_{1}+x_{2})}\geq0$,当且仅当$x_{1}=x_{2}$时取等号,所以$\frac{f(x_{1})+f(x_{2})}{2}\geq f\left(\frac{x_{1}+x_{2}}{2}\right)$,故B错误。因为$g\left(\frac{x_{1}+x_{2}}{2}\right)-\frac{g(x_{1})+g(x_{2})}{2}=\lg\frac{x_{1}+x_{2}}{2}+2-\frac{(\lg x_{1}+2)+(\lg x_{2}+2)}{2}=\lg\frac{x_{1}+x_{2}}{2}-\frac{1}{2}\lg(x_{1}x_{2})=\lg\frac{x_{1}+x_{2}}{2\sqrt{x_{1}x_{2}}}\geq\lg\frac{2\sqrt{x_{1}x_{2}}}{2\sqrt{x_{1}x_{2}}}=0$,当且仅当$x_{1}=x_{2}$时取等号,所以$g\left(\frac{x_{1}+x_{2}}{2}\right)\geq\frac{g(x_{1})+g(x_{2})}{2}$,故C正确。令$h(x)=0$,则有$f(x)=g(x)$,函数$h(x)=f(x)-g(x)$的零点即为函数$f(x)$与函数$g(x)$图像交点的横坐标。在同一平面直角坐标系中,分别画出$f(x)=x+\frac{1}{x}(x\gt0)$和$g(x)=\lg x + 2$的图像,如图所示。
根据函数$f(x)$和$g(x)$的图像可知,函数$h(x)$有且仅有两个零点,故D正确。
选ACD。

13. 函数$y=\frac{1}{3^{x}+2}$的值域为
$\left(0,\frac{1}{2}\right)$
.
答案:
13. $\left(0,\frac{1}{2}\right)$ 【解析】$\because 3^{x}\gt0$,$\therefore 3^{x}+2\gt2$,$\therefore 0\lt\frac{1}{3^{x}+2}\lt\frac{1}{2}$,即$y\in\left(0,\frac{1}{2}\right)$,$\therefore$函数$y=\frac{1}{3^{x}+2}$的值域为$\left(0,\frac{1}{2}\right)$。
14. 已知函数$f(x)=2^{x}-\frac{1}{x}-a$. 若存在$x\in[-2,-1]$,使得$f(x)=0$,则实数$a$的取值范围是
$\left[\frac{3}{4},\frac{3}{2}\right]$
.
答案:
14. $\left[\frac{3}{4},\frac{3}{2}\right]$ 【解析】令$f(x)=0$,即$a = 2^{x}-\frac{1}{x}$,则$a = 2^{x}-\frac{1}{x}$在$[-2,-1]$上有解。因为函数$y = 2^{x}$在$[-2,-1]$上是增函数,$y=\frac{1}{x}$在$[-2,-1]$上是减函数,所以$g(x)=2^{x}-\frac{1}{x}$在$[-2,-1]$上是增函数,所以$g(x)$在$x = -1$时取得最大值为$2^{-1}-\frac{1}{-1}=\frac{3}{2}$,$g(x)$在$x = -2$时取得最小值$2^{-2}-\frac{1}{-2}=\frac{3}{4}$,即$x\in[-2,-1]$时,$g(x)=2^{x}-\frac{1}{x}\in\left[\frac{3}{4},\frac{3}{2}\right]$,所以实数$a$的取值范围是$\left[\frac{3}{4},\frac{3}{2}\right]$。
15. [2022·山西太原高一期末]已知实数$x_{1}$满足$x+\ln x = 2$,$x_{2}$满足$\ln(1 - x)=x + 1$,则$x_{1}+x_{2}=$
$1$
.
答案:
15. $1$ 思维路径:令$1 - x_{2}=t\stackrel{\ln(1 - x_{2})=x_{2}+1}{\to}\ln t + t = 2\to$令$f(x)=\ln x + x\to$判断$f(x)$的单调性$\to$得到$t = x_{1}\to$求得$x_{1}+x_{2}$的值。
【解析】由题意可知$x_{1}+\ln x_{1}=2$,$\ln(1 - x_{2})=x_{2}+1$。令$1 - x_{2}=t$,则$1 - t = x_{2}$,$\ln t + t = 2$。令$f(x)=\ln x + x$,函数$f(x)=\ln x + x$在$(0,+\infty)$上为增函数,由此可知$t = x_{1}$,即$1 - x_{2}=x_{1}$,$x_{1}+x_{2}=1$。
【解析】由题意可知$x_{1}+\ln x_{1}=2$,$\ln(1 - x_{2})=x_{2}+1$。令$1 - x_{2}=t$,则$1 - t = x_{2}$,$\ln t + t = 2$。令$f(x)=\ln x + x$,函数$f(x)=\ln x + x$在$(0,+\infty)$上为增函数,由此可知$t = x_{1}$,即$1 - x_{2}=x_{1}$,$x_{1}+x_{2}=1$。
16. [2022·天津南开中学高一期末]已知函数$f(x)=\begin{cases}x^{2}+(3 - a)x + a,x < 1,\\x-\ln a,x\geq1\end{cases}$若$\forall x\in\mathbf{R}$,不等式$f(x)\geq0$恒成立,则$a$的取值范围是 ______ .
答案:
16. $[1,e]$ 【解析】因为$\forall x\in\mathbf{R}$,不等式$f(x)\geq0$恒成立,所以当$x\geq1$时,$x - \ln a\geq0$恒成立,即$\ln a$小于或等于$x$的最小值1,所以$0\lt a\leq e$;当$x\lt1$时,$x^{2}+(3 - a)x + a\geq0$恒成立,即$a$大于或等于$\left(\frac{-x^{2}-3x}{1 - x}\right)$的最大值。令$1 - x = t(t\gt0)$,则$\frac{-x^{2}-3x}{1 - x}=\frac{-(1 - t)^{2}-3(1 - t)}{t}=\frac{-t^{2}+2t - 1 - 3 + 3t}{t}=-\left(t+\frac{4}{t}\right)+5$。$\because t\gt0$,$\therefore t+\frac{4}{t}\geq2\sqrt{t×\frac{4}{t}} = 4$,当且仅当$t=\frac{4}{t}=2$时等号成立,$\therefore -\left(t+\frac{4}{t}\right)+5\leq1$,$\therefore a\geq1$。综上所述,$a$的取值范围是$[1,e]$。
17. (本小题满分 10 分)计算:
(1)$[(1-\log_{6}3)^{2}+\log_{6}2×\log_{6}18]×\log_{4}6$;
(2)$\vert(\frac{4}{9})^{-\frac{1}{2}}-\lg5\vert+\sqrt{(\lg2)^{2}-\lg4 + 1}-3^{1-\log_{3}2}$.
(1)$[(1-\log_{6}3)^{2}+\log_{6}2×\log_{6}18]×\log_{4}6$;
(2)$\vert(\frac{4}{9})^{-\frac{1}{2}}-\lg5\vert+\sqrt{(\lg2)^{2}-\lg4 + 1}-3^{1-\log_{3}2}$.
答案:
17.【解】
(1)原式$=\left[1 - 2\log_{6}3 + (\log_{6}3)^{2}+\log_{6}\frac{6}{3}×\log_{6}(6×3)\right]×\log_{4}6=\left[1 - 2\log_{6}3 + (\log_{6}3)^{2}+(1 - \log_{6}3)(1 + \log_{6}3)\right]×\log_{4}6=\left[1 - 2\log_{6}3 + (\log_{6}3)^{2}+1 - (\log_{6}3)^{2}\right]×\log_{4}6 = 2(1 - \log_{6}3)×\log_{4}6=\frac{2(1 - \log_{6}3)}{\log_{6}4}×\log_{6}6=\frac{\log_{6}6 - \log_{6}3}{\log_{6}2}=\frac{\log_{6}2}{\log_{6}2}=1$。
(2)原式$=\left\vert\left[\left(\frac{2}{3}\right)^{2}\right]^{\frac{1}{2}}-\lg5\right\vert+\sqrt{(\lg2)^{2}-2\lg2 + 1}-3×3^{-\log_{3}2}=\left\vert\frac{3}{2}-\lg5\right\vert+\vert\lg2 - 1\vert-\frac{3}{2}=\frac{3}{2}-\lg5 + 1 - \lg2 - \frac{3}{2}=1 - (\lg2 + \lg5)=1 - \lg10 = 0$。
(1)原式$=\left[1 - 2\log_{6}3 + (\log_{6}3)^{2}+\log_{6}\frac{6}{3}×\log_{6}(6×3)\right]×\log_{4}6=\left[1 - 2\log_{6}3 + (\log_{6}3)^{2}+(1 - \log_{6}3)(1 + \log_{6}3)\right]×\log_{4}6=\left[1 - 2\log_{6}3 + (\log_{6}3)^{2}+1 - (\log_{6}3)^{2}\right]×\log_{4}6 = 2(1 - \log_{6}3)×\log_{4}6=\frac{2(1 - \log_{6}3)}{\log_{6}4}×\log_{6}6=\frac{\log_{6}6 - \log_{6}3}{\log_{6}2}=\frac{\log_{6}2}{\log_{6}2}=1$。
(2)原式$=\left\vert\left[\left(\frac{2}{3}\right)^{2}\right]^{\frac{1}{2}}-\lg5\right\vert+\sqrt{(\lg2)^{2}-2\lg2 + 1}-3×3^{-\log_{3}2}=\left\vert\frac{3}{2}-\lg5\right\vert+\vert\lg2 - 1\vert-\frac{3}{2}=\frac{3}{2}-\lg5 + 1 - \lg2 - \frac{3}{2}=1 - (\lg2 + \lg5)=1 - \lg10 = 0$。
查看更多完整答案,请扫码查看


