2025年练习生高中数学必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
20. [2022·浙江衢州高一期末]已知函数 $ f(x) = x^{3} + \frac{2^{x} - 1}{2^{x} + 1} $,则不等式 $ f(x - 2) + f(x^{2} - 4) < 0 $ 的解集为(
A.$ (-3, 2) $
B.$ (-2, 3) $
C.$ (-1, 6) $
D.$ (-6, 1) $
A
)A.$ (-3, 2) $
B.$ (-2, 3) $
C.$ (-1, 6) $
D.$ (-6, 1) $
答案:
20. A 思维路径:判断函数f(x)的奇偶性→判断函数y = x^3,y = -$\frac{2}{2^x + 1}$的单调性→得出函数f(x)的单调性→根据函数的单调性,结合奇偶性去掉函数符号→解不等式得结果。
[解析]因为函数f(x)的定义域为R,且f(-x)=(-x)^3 + $\frac{2^(-x) - 1}{2^(-x) + 1}$=-x^3 - $\frac{2^x - 1}{2^x + 1}$=-f(x),所以函数f(x)为奇函数。f(x)=x^3 + $\frac{2^x - 1}{2^x + 1}$=x^3 + 1 - $\frac{2}{2^x + 1}$。因为函数y = x^3,y = -$\frac{2}{2^x + 1}$在(0,+∞)上都是增函数,所以函数f(x)在(0,+∞)上是增函数。又因为函数f(x)的定义域为R且函数是奇函数,所以函数f(x)在R上单调递增。因为f(x - 2) + f(x^2 - 4)<0,所以f(x - 2)< -f(x^2 - 4)=f(4 - x^2),所以x - 2<4 - x^2,即x^2 + x - 6<0,解得 - 3<x<2,即不等式f(x - 2) + f(x^2 - 4)<0的解集为(-3,2)。故选A。
[解析]因为函数f(x)的定义域为R,且f(-x)=(-x)^3 + $\frac{2^(-x) - 1}{2^(-x) + 1}$=-x^3 - $\frac{2^x - 1}{2^x + 1}$=-f(x),所以函数f(x)为奇函数。f(x)=x^3 + $\frac{2^x - 1}{2^x + 1}$=x^3 + 1 - $\frac{2}{2^x + 1}$。因为函数y = x^3,y = -$\frac{2}{2^x + 1}$在(0,+∞)上都是增函数,所以函数f(x)在(0,+∞)上是增函数。又因为函数f(x)的定义域为R且函数是奇函数,所以函数f(x)在R上单调递增。因为f(x - 2) + f(x^2 - 4)<0,所以f(x - 2)< -f(x^2 - 4)=f(4 - x^2),所以x - 2<4 - x^2,即x^2 + x - 6<0,解得 - 3<x<2,即不等式f(x - 2) + f(x^2 - 4)<0的解集为(-3,2)。故选A。
21. (多选)[2022·江苏常州高一学业水平监测]若函数 $ f(x) = a^{x} (a > 0 $,且 $ a \neq 1) $ 在区间 $ [-2, 2] $ 上的最大值和最小值的和为 $ \frac{10}{3} $,则 $ a $ 的值可能是(
A.$ \frac{1}{3} $
B.$ \frac{\sqrt{3}}{3} $
C.$ \sqrt{3} $
D.$ 3 $
BC
)A.$ \frac{1}{3} $
B.$ \frac{\sqrt{3}}{3} $
C.$ \sqrt{3} $
D.$ 3 $
答案:
21. BC [解析]当0<a<1时,函数f(x)=a^x在[-2,2]上为减函数,函数的最小值为f
(2)=a^2,函数的最大值为f(-2)=a^(-2)=$\frac{1}{a^2}$,此时$\frac{1}{a^2}$ + a^2 = $\frac{10}{3}$,解得a = $\frac{\sqrt{3}}{3}$;当a>1时,函数f(x)=a^x在[-2,2]上为增函数,函数的最大值为f
(2)=a^2,函数的最小值为f(-2)=a^(-2)=$\frac{1}{a^2}$,此时a^2 + $\frac{1}{a^2}$ = $\frac{10}{3}$,解得a = $\sqrt{3}$。综上所述,a = $\frac{\sqrt{3}}{3}$或a = $\sqrt{3}$,故选BC。
(2)=a^2,函数的最大值为f(-2)=a^(-2)=$\frac{1}{a^2}$,此时$\frac{1}{a^2}$ + a^2 = $\frac{10}{3}$,解得a = $\frac{\sqrt{3}}{3}$;当a>1时,函数f(x)=a^x在[-2,2]上为增函数,函数的最大值为f
(2)=a^2,函数的最小值为f(-2)=a^(-2)=$\frac{1}{a^2}$,此时a^2 + $\frac{1}{a^2}$ = $\frac{10}{3}$,解得a = $\sqrt{3}$。综上所述,a = $\frac{\sqrt{3}}{3}$或a = $\sqrt{3}$,故选BC。
22. (多选)[2022·浙江绿谷高中联盟高一期中]已知函数 $ y = a^{x}, y = b^{x} (a, b > 0 $ 且 $ a \neq 1, b \neq 1) $ 的图像如图所示,则下列结论正确的是(
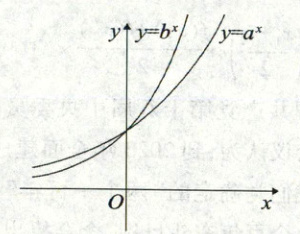
A.$ a > b > 1 $
B.$ 0 < a < b < 1 $
C.$ 2^{a} < 2^{b} $
D.$ b > a > 1 $
CD
)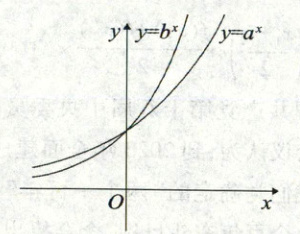
A.$ a > b > 1 $
B.$ 0 < a < b < 1 $
C.$ 2^{a} < 2^{b} $
D.$ b > a > 1 $
答案:
22. CD [解析]由指数函数图像可知b>a>1,故A错误,B错误,D正确;由b>a>1可得2^a<2^b,故C正确。选CD。
23. 函数 $ f(x) = 4^{x} - 2^{x + 1} $ 的值域是
[-1,+∞)
。
答案:
23. [-1,+∞) [解析]令t = 2^x>0,则$f(x)=(2^x)^2 - 2×2^x = t^2 - 2t = (t - 1)^2 - 1≥ - 1,$函数f(x)的值域为[-1,+∞)。
24. 已知点 $ P(-1, \frac{\sqrt{2}}{2}), Q(m, 2) $ 均在指数函数的图像上,则 $ m $ 的值为
2
。
答案:
24. 2 [解析]设所求的指数函数为y = a^x(a>0,a≠1)。
∵P(-1,$\frac{\sqrt{2}}{2}$)在指数函数图像上,
∴$\frac{\sqrt{2}}{2}$=$\frac{1}{a}$,
∴a = $\sqrt{2}$,则y = ($\sqrt{2}$)^x。将Q(m,2)的坐标代入解析式,得2 = ($\sqrt{2}$)^m,解得m = 2。
∵P(-1,$\frac{\sqrt{2}}{2}$)在指数函数图像上,
∴$\frac{\sqrt{2}}{2}$=$\frac{1}{a}$,
∴a = $\sqrt{2}$,则y = ($\sqrt{2}$)^x。将Q(m,2)的坐标代入解析式,得2 = ($\sqrt{2}$)^m,解得m = 2。
25. [2022·北京海淀高一期末]写出定义域为 $ \mathbf{R} $,值域为 $ (-\infty, 1) $ 的一个减函数
f(x)=1 - 2^x(答案不唯一)
。
答案:
25. f(x)=1 - 2^x(答案不唯一) [解析]因为f(x)=2^x的定义域为R,在R上是增函数,且值域为(0,+∞),所以f(x)= -2^x的定义域为R,在R上是减函数,且值域为(-∞,0),所以f(x)=1 - 2^x的定义域为R,在R上是减函数,且值域为(-∞,1)。本题答案不唯一。
26. [2022·宁夏吴忠中学高一期末]已知函数 $ f(x) = (\frac{1}{2})^{x^{2} - 2x + 5} $ 在 $ (a, +\infty) $ 上单调递减,则实数 $ a $ 的取值范围是
[1,+∞)
。
答案:
26. [1,+∞) [解析]令g(x)=x^2 - 2x + 5,其对称轴为x = 1,则函数g(x)在(-∞,1]上单调递减,在[1,+∞)上单调递增。因为函数f(x)=($\frac{1}{2}$)^(x^2 - 2x + 5),所以根据复合函数的单调性的判定方法,可得函数f(x)在(-∞,1]上单调递增,在[1,+∞)上单调递减。又因为函数f(x)在(a,+∞)上单调递减,所以a≥1,所以实数a的取值范围是[1,+∞)。
27. 若直线 $ y = 2a $ 与函数 $ y = |a^{x} - 1| (a > 0, a \neq 1) $ 的图像有两个公共点,则 $ a $ 的取值范围是
(0,$\frac{1}{2}$)
。
答案:
27. (0,$\frac{1}{2}$) [解析]方法一:因为直线y = 2a与y = |a^x - 1|(a>0,a≠1)的图像有两个公共点,所以|a^x - 1|=2a有两个不同的解,所以$\begin{cases}a^x\geq1\\a^x = 2a + 1\end{cases}$和$\begin{cases}0< a^x<1\\a^x = -2a + 1\end{cases}$共有两个不同的解。因为2a + 1>1,所以$\begin{cases}a^x\geq1\\a^x = 2a + 1\end{cases}$有且只有一个实数解。若a>1,则1 - 2a<0,$\begin{cases}0< a^x<1\\a^x = -2a + 1\end{cases}$无解,而$\begin{cases}a^x≥1\\a^x = 2a + 1\end{cases}$只有一个解,因此|a^x - 1|=2a有且只有一个实数解,与题设矛盾,即a>1不符合题意;若0<a<1,因为$\begin{cases}a^x≥1\\a^x = 2a + 1\end{cases}$只有一个解,所以$\begin{cases}0< a^x<1\\a^x = -2a + 1\end{cases}$需有一解,所以0<1 - 2a<1,解得0<a<$\frac{1}{2}$。
方法二:当0<a<1时,函数y = |a^x - 1|的图像如图(1)所示。若直线y = 2a与函数y = |a^x - 1|的图像有两个公共点,由图像可知0<2a<1,即0<a<$\frac{1}{2}$;


当a>1时,函数y = |a^x - 1|的图像如图(2)所示,此时2a>2,直线y = 2a与函数y = |a^x - 1|的图像只有一个公共点。
综上所述,a的取值范围是(0,$\frac{1}{2}$)。
27. (0,$\frac{1}{2}$) [解析]方法一:因为直线y = 2a与y = |a^x - 1|(a>0,a≠1)的图像有两个公共点,所以|a^x - 1|=2a有两个不同的解,所以$\begin{cases}a^x\geq1\\a^x = 2a + 1\end{cases}$和$\begin{cases}0< a^x<1\\a^x = -2a + 1\end{cases}$共有两个不同的解。因为2a + 1>1,所以$\begin{cases}a^x\geq1\\a^x = 2a + 1\end{cases}$有且只有一个实数解。若a>1,则1 - 2a<0,$\begin{cases}0< a^x<1\\a^x = -2a + 1\end{cases}$无解,而$\begin{cases}a^x≥1\\a^x = 2a + 1\end{cases}$只有一个解,因此|a^x - 1|=2a有且只有一个实数解,与题设矛盾,即a>1不符合题意;若0<a<1,因为$\begin{cases}a^x≥1\\a^x = 2a + 1\end{cases}$只有一个解,所以$\begin{cases}0< a^x<1\\a^x = -2a + 1\end{cases}$需有一解,所以0<1 - 2a<1,解得0<a<$\frac{1}{2}$。
方法二:当0<a<1时,函数y = |a^x - 1|的图像如图(1)所示。若直线y = 2a与函数y = |a^x - 1|的图像有两个公共点,由图像可知0<2a<1,即0<a<$\frac{1}{2}$;


当a>1时,函数y = |a^x - 1|的图像如图(2)所示,此时2a>2,直线y = 2a与函数y = |a^x - 1|的图像只有一个公共点。
综上所述,a的取值范围是(0,$\frac{1}{2}$)。
28. 函数 $ f(x) = |2^{x} - 1| $。
(1) 请在下面坐标系中画出函数 $ f(x) $ 的图像。
(2) 不等式 $ f(x) < \frac{1}{4}x + \frac{3}{4} $ 的解集为
(3) 若 $ m < n $,$ f(m) = f(n) $,求 $ m + n $ 的取值范围。
(1) 请在下面坐标系中画出函数 $ f(x) $ 的图像。
(2) 不等式 $ f(x) < \frac{1}{4}x + \frac{3}{4} $ 的解集为
(-1,1)
(写出结果即可,不需写过程)。(3) 若 $ m < n $,$ f(m) = f(n) $,求 $ m + n $ 的取值范围。
答案:
28. [解]
(1)列表如下。
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| --- | --- | --- | --- | --- | --- |
| $f(x)$ | $\frac{3}{4}$ | $\frac{1}{2}$ | $0$ | $1$ | $3$ |
函数f(x)的图像如下。

(2)由
(1)所得f(x)的图像中画出直线y = $\frac{x}{4}$ + $\frac{3}{4}$,可得如下图像(与方程、不等式有关的问题,应联系函数的有关知识,利用函数图像来解决)。

∵y = $\frac{x}{4}$ + $\frac{3}{4}$过点(-1,$\frac{1}{2}$),(1,1),
∴不等式f(x)<$\frac{1}{4}$x + $\frac{3}{4}$的解集为(-1,1)。
(3)
∵f(m)=f(n),
∴|2^m - 1|=|2^n - 1|。
不妨设m<0<n,则1 - 2^m = 2^n - 1,即2^m + 2^n = 2。
∵m<n,
∴2^m≠2^n,
∴2^m + 2^n>2$\sqrt{2^m×2^n}$=2$\sqrt{2^(m + n)}$
∴2^(m + n)<1,
∴m + n<0。
28. [解]
(1)列表如下。
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| --- | --- | --- | --- | --- | --- |
| $f(x)$ | $\frac{3}{4}$ | $\frac{1}{2}$ | $0$ | $1$ | $3$ |
函数f(x)的图像如下。

(2)由
(1)所得f(x)的图像中画出直线y = $\frac{x}{4}$ + $\frac{3}{4}$,可得如下图像(与方程、不等式有关的问题,应联系函数的有关知识,利用函数图像来解决)。

∵y = $\frac{x}{4}$ + $\frac{3}{4}$过点(-1,$\frac{1}{2}$),(1,1),
∴不等式f(x)<$\frac{1}{4}$x + $\frac{3}{4}$的解集为(-1,1)。
(3)
∵f(m)=f(n),
∴|2^m - 1|=|2^n - 1|。
不妨设m<0<n,则1 - 2^m = 2^n - 1,即2^m + 2^n = 2。
∵m<n,
∴2^m≠2^n,
∴2^m + 2^n>2$\sqrt{2^m×2^n}$=2$\sqrt{2^(m + n)}$
∴2^(m + n)<1,
∴m + n<0。
查看更多完整答案,请扫码查看


