《2025年同步练习册人民教育出版社九年级数学上册人教版新疆用》

1. 正$n$边形的一个内角的度数是$\frac{(n-2)\cdot 180°}{n}$；中心角的度数是$\frac{360°}{n}$；正多边形的中心角与外角的大小关系是相等。

答案： $\frac{(n-2)\cdot 180°}{n}$ $\frac{360°}{n}$ 相等

2. 若点$O是等边三角形ABC$的中心,则点$O是\triangle ABC$的内切圆与外接圆的圆心。

答案： 内切 外接

3. 若正多边形的一个中心角为$36^{\circ}$,则这个正多边形的一个内角的度数为144°。

答案： $144°$

4. 某正多边形的每个内角比其外角大$100^{\circ}$,求这个正多边形的边数。

答案： 9

5. 正六边形$ABCDEF外切于\odot O$,若$\odot O的半径为r$,则该正六边形的周长和面积各是多少？

答案： 周长为 $4\sqrt{3}r$，面积为 $2\sqrt{3}r^2$.

6. 用等分圆周的方法画出下列图案：

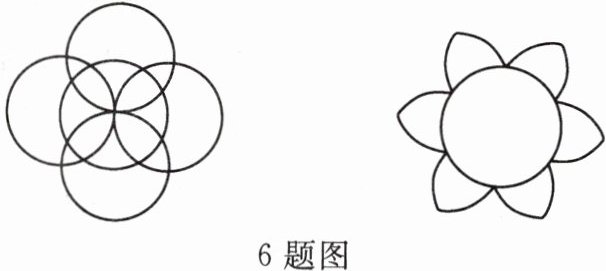
答案：