《2025年同步练习册人民教育出版社九年级数学上册人教版新疆用》

1. 设$\odot O的半径为3$,点$O到直线l的距离为d$,若直线$l与\odot O$只有一个公共点,则$d$应满足的条件是(A).
A.$d = 3$
B.$d \leq 3$
C.$d ＜ 3$
D.$d ＞ 3$

答案： A

2. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 3\mathrm{cm}$,$BC = 4\mathrm{cm}$,给出下列三个结论：
①以点$C$为圆心,$2.3\mathrm{cm}长为半径的圆与AB$相离；
②以点$C$为圆心,$2.4\mathrm{cm}长为半径的圆与AB$相切；
③以点$C$为圆心,$2.5\mathrm{cm}长为半径的圆与AB$相交.
则上述结论正确的有(D).
A.$0$个
B.$1$个
C.$2$个
D.$3$个

答案： D

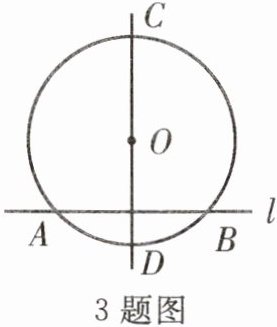
3. 如图,$\odot O的半径为5\mathrm{cm}$,直线$CD$经过圆心,直线$l与直线CD$垂直,交$\odot O于A$,$B$两点,且$AB = 8\mathrm{cm}$,如果直线$l与\odot O$相切,那么直线$l$应平移(D).

A.$3\mathrm{cm}$
B.$2\mathrm{cm}$
C.$8\mathrm{cm}$
D.$2\mathrm{cm}或8\mathrm{cm}$

答案： D

4. 在平面直角坐标系中,以点$(2,3)$为圆心,$2$为半径的圆必定(A).
A.与$x$轴相离,与$y$轴相切
B.与$x$轴、$y$轴都相离
C.与$x$轴相切,与$y$轴相离
D.与$x$轴、$y$轴都相切

答案： A

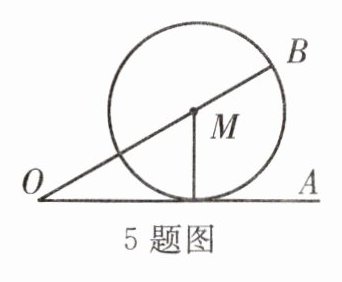
5. 如图,$\angle AOB = 30^{\circ}$,$M为OB$边上一点,以点$M$为圆心,$2\mathrm{cm}为半径作\odot M$,若点$M在OB$边上运动,则当$OM = $4$\mathrm{cm}$时,$\odot M与OA$相切.

答案： 4

6. 如图,已知线段$OA交\odot O于点B$,且$OB = AB$,点$P是\odot O$上的一个动点,则$\angle OAP$的最大值是$30^{\circ}$.

答案： $30^{\circ}$

7. 如图,直线$AB$,$CD相交于点O$,$\angle AOC = 30^{\circ}$,半径为$1\mathrm{cm}的\odot P的圆心在射线OA$上,开始时,$PO = 6\mathrm{cm}$,若$\odot P以1\mathrm{cm/s}的速度从点A向点B$的方向移动,则当$\odot P的运动时间t$(单位：$s$)满足$4＜t＜8$时,$\odot P与直线CD$相交.

答案： $4＜t＜8$