《2025年同步练习册人民教育出版社九年级数学上册人教版新疆用》

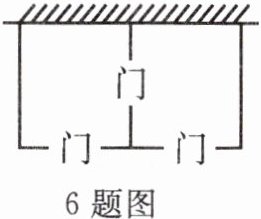
6. 如图所示,某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在三处各留 $ 1 \, m $ 宽的门。已知计划中的材料可建墙体(不包括门)总长为 $ 27 \, m $,求能建成的饲养室总占地最大面积。
]

答案： $75\ m^{2}$

7. 某超市经销一种成本为 $ 40 $ 元/件的商品,据市场调查分析,如果按 $ 50 $ 元/件销售,那么一周能售出 $ 500 $ 件；若销售单价每涨 $ 1 $ 元,则每周销售量就减少 $ 10 $ 件。设销售单价为 $ x $ 元($ x \geq 50 $),一周的销售量为 $ y $ 件。
(1) 写出 $ y $ 关于 $ x $ 的函数解析式(标明 $ x $ 的取值范围)；
(2) 设一周的销售利润为 $ S $,写出 $ S $ 关于 $ x $ 的函数解析式,并确定当单价在什么范围内变化时,利润随单价的增大而增大；
(3) 在超市对该种商品投入不超过 $ 10000 $ 元的情况下,要使得一周销售利润达到 $ 8000 $ 元,销售单价应定为多少？

答案：

$解： (1)由题意得： y=500 - 10(x - 50)$

$∴y=1000 - 10x(50≤x≤100)$

$(2)S=(x - 40)(1000 - 10x)=- 10(x- 70)^2 +9000$

$当50≤x≤70时，利润随着单价的增大而增大$

$(3)由题意得： - 10x^2+ 1400x - 4000= 8000$

$x^2- 140x+ 4800=0$

$即(x- 60)(x - 80)=0$

$x_{1}=60，x_{2}=80$

$当x=60时$

$成本=40×[500 - 10(60 - 50)]=16000\gt 10000$

$不符合要求，舍去$

$当x=80时$

$成本=40×[500 - 10(80 - 50)]=8000 \lt 10000$

$符合要求$

$∴销售单价应定为80元，才能使得一周销售$

$利润达到8000元的同时，投入不超过10000元$