《2025年同步练习册人民教育出版社九年级数学上册人教版新疆用》

6. 教室里的三叶吊扇至少旋转120°后才能与自身重合.

答案： $120^{\circ}$

7. 已知平面直角坐标系中的三个点 $ O(0, 0) $,$ A(-1, 1) $,$ B(-1, 0) $,若将 $ \triangle ABO $ 绕点 $ O $ 顺时针旋转 $ 135° $,则点 $ A $,$ B $ 的对应点 $ A_1 $,$ B_1 $ 的坐标分别是$(\sqrt{2},0)$，$(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$.

答案： $(\sqrt{2},0)$，$(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$

8. 在一个 $ 6 × 8 $ 的矩形地块上,欲开辟出一部分建花坛,要使花坛的面积为矩形的一半,请给出你的设计方案(至少两种).

答案： 方案一
沿矩形地块的长（8单位）方向，取中点将矩形分为两个全等的小矩形。
花坛面积：$6 × (8 ÷ 2) = 6 × 4 = 24$，矩形面积：$6 × 8 = 48$，$24 = 48 × \frac{1}{2}$。
方案二
连接矩形地块一组对边的中点，形成一个平行四边形花坛（以原矩形的宽为底，高为长的一半）。
花坛面积：$6 × (8 ÷ 2) = 24$，满足面积为矩形一半。
方案三
在矩形内画一个三角形花坛，以矩形的长（8）为底，宽（6）为高。
花坛面积：$\frac{1}{2} × 8 × 6 = 24$，满足面积为矩形一半。
（注：任选两种即可，以上为示例方案）

9. 在中国的园林建筑中,很多建筑图形具有对称性. 下图是一个破损的花窗图形,请把它补画成中心对称图形.

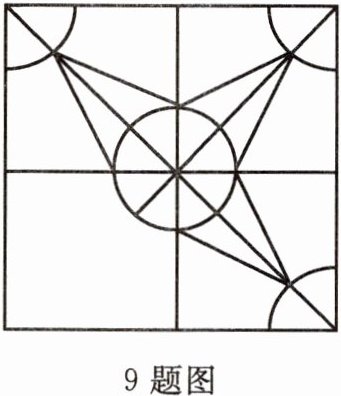
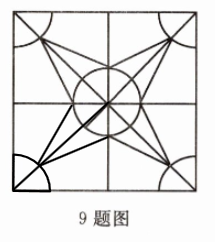
答案：

10. 如图,有 8 个小正方形,怎样分割才能恰好拼成一个大正方形?

答案：

11. 某地板厂要制作一批正六边形的地板砖(如图所示),为了适应市场多样化的需求,要求在地板砖上设计的图案能够把正六边形六等分,请你帮助他们设计等分图案(至少设计两种).

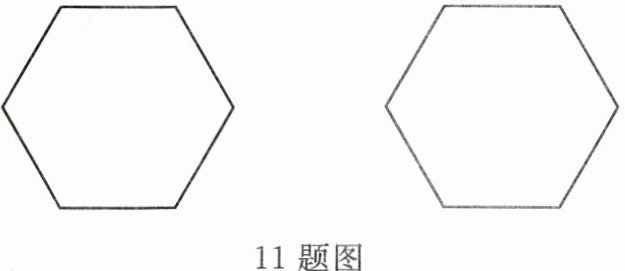
答案：
答案不唯一，例如:

12. 如图,只移动 3 个小三角形,怎样由甲图变为乙图?

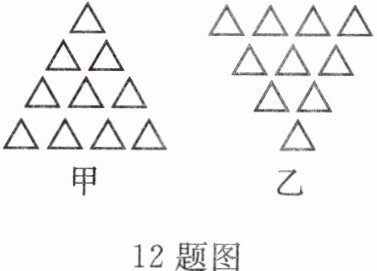
答案：