《2025年同步练习册人民教育出版社九年级数学上册人教版新疆用》

6. 在等腰直角三角形$ABC$中,$\angle C= 90^{\circ}$,$BC= 2\mathrm{cm}$,以$AC的中点O$为旋转中心,把这个三角形旋转$180^{\circ}$,点$B旋转至点B'$处,求点$B'与点B$之间的距离.

答案： $2\sqrt{5}\,cm$

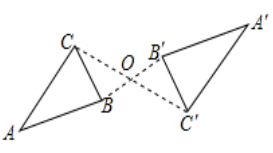
7. 如图,$\triangle ABC与\triangle A'B'C'关于点O$中心对称,但点$O$不慎被涂掉了,请找到对称中心$O$的位置.

答案：
根据中心对称的性质，连结两组对应点$AA'$和$BB'$（或$CC'$），连线的交点即为对称中心$O$。
具体步骤如下：
连结$AA'$、$BB'$。
$AA'$与$BB'$相交于点$O$。
则点$O$即为对称中心。
最终答案即点$O$为$AA'$与$BB'$的交点。

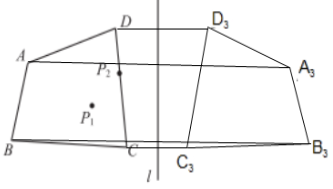
8. 如图,点$P_1在四边形ABCD$的内部,点$P_2在边CD$上,直线$l在四边形ABCD$外.
(1)画出四边形$ABCD关于点P_1对称的四边形A_1B_1C_1D_1$.
(2)画出四边形$ABCD关于点P_2对称的四边形A_2B_2C_2D_2$.
(3)画出四边形$ABCD关于直线l对称的四边形A_3B_3C_3D_3$.(不写画法)

答案：

9. 为了方便记忆,$26$个英文字母可以尝试分成五类.现在还剩下$5个字母D$,$M$,$Q$,$X$,$Z$,请你根据现有的分类信息把这$5$个字母分别填在相应的方框中.
(1)$F$ $R$ $P$ $J$ $L$ $G$ $Q$
(2)$H$ $I$ $O$ $X$
(3)$N$ $S$ $Z$
(4)$B$ $C$ $K$ $E$ $D$
(5)$V$ $A$ $T$ $Y$ $W$ $U$ $M$

答案：
(1)Q
(2)X
(3)Z
(4)D
(5)M