《2025年同步练习册人民教育出版社九年级数学上册人教版新疆用》

15. 根据下面的问题设未知数列出方程,并将其化为一般形式.
某市要组织一次篮球邀请赛,参赛的每两个队之间都要比赛一场. 根据场地和时间等条件,赛程计划安排 $ 7 $ 天,每天安排 $ 4 $ 场比赛,比赛组织者应邀请多少个队参赛？

答案： 解：设邀请x个队参加，则$\frac{x(x-1)}{2}=4×7$，化为一般形式，得$x²-x-56=0$.

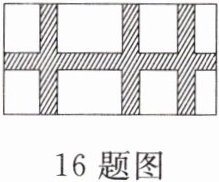
16. 在长为 $ 32 \, m $、宽为 $ 20 \, m $ 的长方形耕地上,修同样宽的四条道路(如图所示),把耕地分为大小不等的长方形试验地,耕地总面积为 $ 551 \, m^2 $,道路应修多宽？(只列方程)

答案： 解：设道路宽为x m，所以(32-3x)(20-x)=551.

1. 根据平方根的意义,求$x$的值：
$x^{2}= 3$；
$3x^{2}-5= 13$；
$(x + 1)^{2}= 8$；
$(x - 2)^{2}+2= 11$。

答案： $(1)$求解$x^{2}=3$
解：根据平方根的意义，若$x^{2}=a$（$a\geq0$），则$x = \pm\sqrt{a}$。
对于$x^{2}=3$，这里$a = 3$，所以$x=\pm\sqrt{3}$。
$(2)$求解$3x^{2}-5 = 13$
解：
首先对$3x^{2}-5 = 13$进行移项，得到$3x^{2}=13 + 5$。
计算$13 + 5=18$，则方程变为$3x^{2}=18$。
两边同时除以$3$，即$x^{2}=\frac{18}{3}=6$。
再根据平方根的意义，$x=\pm\sqrt{6}$。
$(3)$求解$(x + 1)^{2}=8$
解：
根据平方根的意义，若$y^{2}=a$（$a\geq0$），则$y=\pm\sqrt{a}$，这里令$y=x + 1$，$a = 8$，所以$x + 1=\pm\sqrt{8}$。
化简$\sqrt{8}=\sqrt{4×2}=2\sqrt{2}$，则$x + 1=\pm2\sqrt{2}$。
移项可得$x=-1\pm2\sqrt{2}$，即$x=-1 + 2\sqrt{2}$或$x=-1-2\sqrt{2}$。
$(4)$求解$(x - 2)^{2}+2 = 11$
解：
先对$(x - 2)^{2}+2 = 11$进行移项，得到$(x - 2)^{2}=11 - 2$。
计算$11 - 2 = 9$，则方程变为$(x - 2)^{2}=9$。
根据平方根的意义，$x - 2=\pm\sqrt{9}$。
因为$\sqrt{9}=3$，所以$x - 2=\pm3$。
当$x - 2 = 3$时，$x=3 + 2=5$；当$x - 2=-3$时，$x=-3 + 2=-1$。
综上，$(1)$$\boldsymbol{x=\pm\sqrt{3}}$；$(2)$$\boldsymbol{x=\pm\sqrt{6}}$；$(3)$$\boldsymbol{x=-1\pm2\sqrt{2}}$；$(4)$$\boldsymbol{x = 5}$或$\boldsymbol{x=-1}$。