《2025年同步练习册人民教育出版社九年级数学上册人教版新疆用》

9. 如图,⊙O 的直径 AB 和弦 CD 相交于点 E,AE = 2,EB = 6,∠DEB = 30°,求弦 CD 的长。

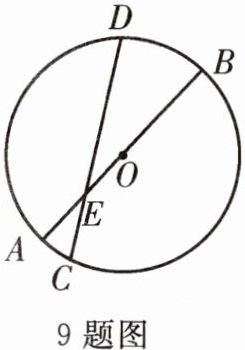
答案： 解：过点 O 作 OF⊥CD 于点 F，
∵AE=2，BE=6，
∴AB=8，
∴OE=2，
∵∠DEB=30°，
∴在Rt△EOF中，OF=1，连接 OD，在Rt△ODF中，$DF=\sqrt{4^2 - 1^2}=\sqrt{15}$，
∴$CD=2\sqrt{15}$.

10. 如图,A,B 是⊙O 上两点,AB = 10,P 是⊙O 上一动点(点 P 与点 A,B 不重合),连接 AP,PB,过点 O 分别作 OE⊥AP 于点 E,OF⊥PB 于点 F,连接 EF,求 EF 的长。

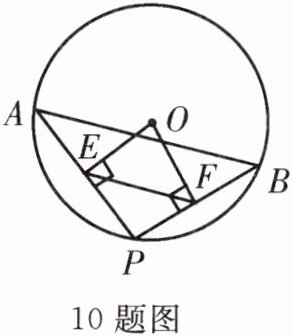
答案： 解：
∵OE⊥AP，OF⊥BP，
∴AE=PE，BF=PF，
∴$EF=\frac{1}{2}AB$.又AB=10，
∴EF=5.

11. 如图,有一座圆弧形的拱桥(示意图),桥下水面宽度 AB 为 7.2 m,拱顶高出水平面 2.4 m,现有一艘宽为 3 m,船舱顶部为正方形并高出水平面 2 m 的货船要经过拱桥,请你判断一下,此货船能顺利通过这座拱桥吗？请说明理由。($\sqrt{2.96}\approx1.72$)

答案： 解：连接 ON，OB.
∵OC⊥AB，
∴D 为 AB 中点，
∵AB=7.2 m，
∴$BD=\frac{1}{2}AB=3.6$ m. 又 CD=2.4 m，设 OB=OC=ON=r m，则 OD=(r - 2.4)m. 在Rt△BOD中，根据勾股定理，得$r^2=(r - 2.4)^2 + 3.6^2$，解得 r=3.9.
∵CD=2.4 m，船舱顶部为正方形并高出水平面 2 m，
∴CE=2.4 - 2=0.4（m），
∴OE=r - CE=3.9 - 0.4=3.5（m），在Rt△OEN中，$EN^2=ON^2 - OE^2=3.9^2 - 3.5^2=2.96$，
∴$EN=\sqrt{2.96}$ m，
∴$MN=2EN=2×\sqrt{2.96}≈3.44$ m＞3 m.
∴此货船能顺利通过这座拱桥.