《2025年同步练习册人民教育出版社九年级数学上册人教版新疆用》

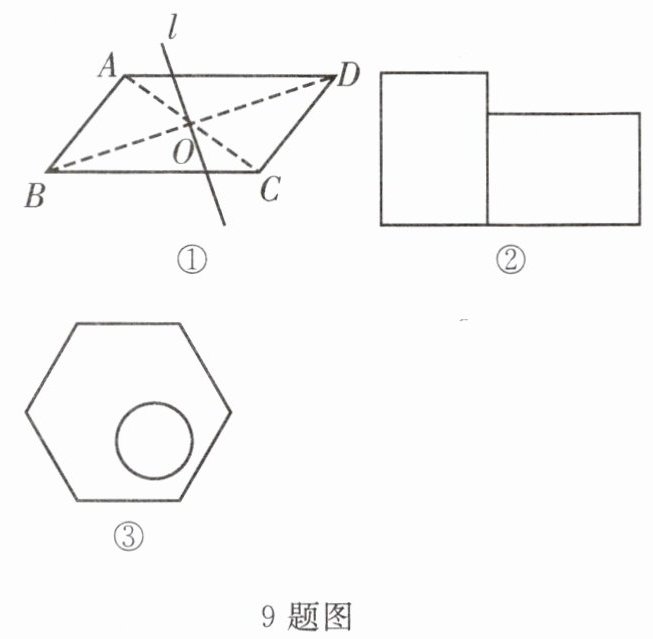
9. 如图①,□ABCD的面积被过其对称中心的直线l平分吗？利用此图得到的启示,试分别作一条直线,使其将图②③分成面积相等的两部分.

答案：
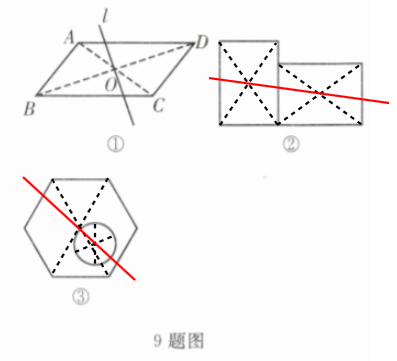
9. 平分。理由：平行四边形是中心对称图形，过对称中心的直线将其面积平分。

10. 某校要在一块圆形空地上建造花园,种四种颜色的花,为了便于管理且美观,相同颜色的花集中种植,且每种颜色的花所占的面积相同,现征集设计方案,要求设计的图案既是轴对称图形,又是中心对称图形,请你设计两种方案.

答案：
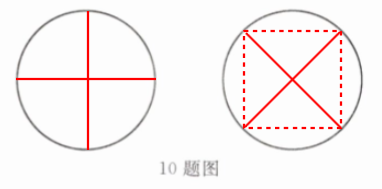
方案一：作圆的两条互相垂直的直径，将圆分成四个全等的扇形，每个扇形种植一种颜色的花。
方案二：作圆的内接正方形，连接正方形的两条对角线（过圆心且互相垂直），将正方形分成四个全等的等腰直角三角形，每个三角形与其相邻的圆和正方形边所夹的弓形组成一个区域，共四个全等区域，每个区域种植一种颜色的花。

1. 在平面直角坐标系中,点 $ A $ 的坐标是 $ (2,-3) $,若点 $ B $ 与点 $ A $ 关于原点 $ O $ 对称,则点 $ B $ 的坐标是(B).
A.$ (2,3) $
B.$ (-2,3) $
C.$ (-2,-3) $
D.$ (2,-3) $

答案： B

2. 如图,$ \triangle DEF $ 是由 $ \triangle ABC $ 经过某种变换后得到的图形,观察各顶点的坐标,可知点 $ A $ 和点 $ D $ 的坐标分别是(3，-2)，(-3，2)；点 $ B $ 和点 $ E $ 的坐标分别是(2，-5)，(-2，5)；点 $ C $ 和点 $ F $ 的坐标分别是(6，-5)，(-6，5),若 $ \triangle ABC $ 边上任意一点 $ M $ 的坐标为 $ (x,y) $,则它对应于 $ \triangle DEF $ 上点的坐标是(-x，-y).

答案： (3，-2)，(-3，2)(2，-5)，(-2，5) (6，-5)，(-6，5) (-x，-y)