《2025年同步练习册人民教育出版社九年级数学上册人教版新疆用》

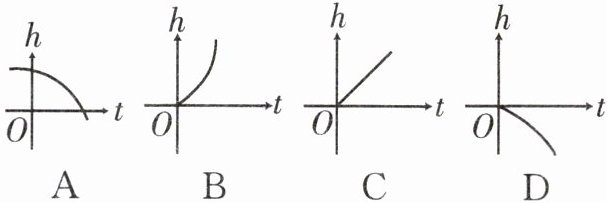
1. 桃子熟了,若从树上落下所经过的路程 $ h $ 与下落的时间 $ t $ 满足 $ h = \frac{1}{2}gt^{2} $($ g $ 是不为 $ 0 $ 的常数),则 $ h $ 关于 $ t $ 的函数图象大致是(B)。

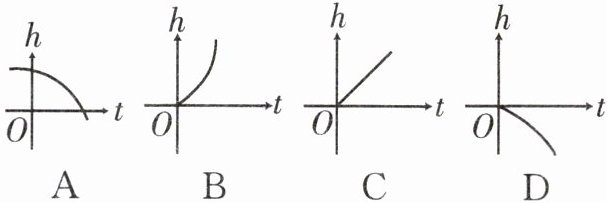
答案： B

2. 从一个边长为 $ 20 \, cm $ 的正方形纸板中剪去一个边长为 $ x $($ 0 ＜ x ＜ 12 $)的正方形和一个边长为 $ \frac{2}{3}x $ 的正方形,剩余纸板的面积 $ y $ 关于 $ x $ 的函数解析式是$y=-\dfrac{13}{9}x^{2}+400$。

答案： $y=-\dfrac{13}{9}x^{2}+400$

3. 某商店以 $ 40 $ 元/件的价格购进了一批服装,按 $ 50 $ 元/件出售时,一周内可售出 $ 100 $ 件；当售价每提高 $ 1 $ 元时,其周销售量就会减少 $ 5 $ 件。若设每件售价为 $ x $ 元,总利润为 $ y $ 元,则 $ y $ 关于 $ x $ 的函数解析式为$y=-5x^{2}+550x-14\ 000$。

答案： $y=-5x^{2}+550x-14\ 000$

4. 某广告公司为客户设计一块周长为 $ 12 $ 米的矩形产品宣传板,宣传板的设计费用为 $ 1000 $ 元/平方米。设矩形的一边为 $ x $ 米,当 $ x = $3时,广告公司获得的设计费用最多。

答案： 3

5. 某商店购进一批单价为 $ 16 $ 元的日用品,销售一段时间后,为了获得更多的利润,该商店决定提高价格,经试销发现,按 $ 20 $ 元/件的价格销售时,每月能卖 $ 360 $ 件；按 $ 25 $ 元/件的价格销售时,每月能卖 $ 210 $ 件。假定每月销售的件数 $ y $(单位：件)是销售价格 $ x $(单位：元/件)的一次函数。
(1) 试求 $ y $ 关于 $ x $ 的函数解析式(不必写出自变量的取值范围)；
(2) 如果按 $ x $ 元/件的价格销售时,每月可获得销售利润 $ W $ 元,试写出 $ W $ 关于 $ x $ 的函数解析式,它是 $ x $ 的二次函数吗？

答案：

$解：(1)设y=kx+b$

$将点(20，360)、(25，210)代入可得$

$\begin{cases}20k+b=360\\25k+b=210\end{cases}$

$解得\begin{cases}k=-30\\b=960\end{cases}$

$∴y=-30x+960$

$(2)W=(x-16)(-30x+960)$

$∴W=-30x^2+1440x-15360$

$∴W是x的二次函数$