《2025年资源与评价黑龙江教育出版社七年级数学上册人教版H》

9. 有只狡猾的狐狸,它平时总喜欢戏弄人,有一天它遇见了老虎,狐狸说：“我发现 2025 和 3 是一样大的。我这里有一个方程：$ 2025x - 2 = 3x - 2 $。①等式两边加上 2,得 $ 2025x - 2 + 2 = 3x - 2 + 2 $,即 $ 2025x = 3x $。②等式两边除以 $ x $,得 $ 2025 = 3 $。”
你认为狐狸的说法正确吗？如果正确,请说明上述①②步的理由；如果不正确,请指出错在哪里,并加以改正。

答案： 解:不正确.步骤①正确,运用了等式的性质1;
步骤②两边除以x错误.
改正:2025x-3x=0,
2022x=0,
x=0.

10. 利用“作差法”可以比较两个数或两个代数式值的大小。若 $ a - b ＞ 0 $,则 $ a ＞ b $；若 $ a - b = 0 $,则 $ a = b $；若 $ a - b ＜ 0 $,则 $ a ＜ b $。
(1) 试比较代数式 $ 5m^2 - 4m + 2 $ 与 $ 4m^2 - 4m - 7 $ 的值的大小关系；
(2) 若 $ A = 5m^2 - 4(\frac{7}{4}m - \frac{1}{2}) $,$ B = 7(m^2 - m) + 3 $,请你运用前面介绍的方法比较代数式 $ A $ 与 $ B $ 的值的大小。

答案： 解:
(1)因为$(5m^{2}-4m+2)-(4m^{2}-4m-7)=m^{2}+9＞0$,
所以$5m^{2}-4m+2＞4m^{2}-4m-7$.
(2)$A-B=5m^{2}-4(\frac{7}{4}m-\frac{1}{2})-[7(m^{2}-m)+3]=-(2m^{2}+1)＜0$,
所以A＜B.

1. 对于任意有理数 $ a $,$ b $,$ c $,$ d $,我们规定 $ \begin{vmatrix}a&b\\c&d\end{vmatrix} = ad - bc $,如 $ \begin{vmatrix}1&2\\3&4\end{vmatrix} = 1×4 - 2×3 = -2 $。若 $ \begin{vmatrix}x&-2\\3&-4\end{vmatrix} = -2 $,则 $ x $ 的值为2。

答案： 2

2. 如图,把一个边长为 $ x $ cm 的正方形铁皮的四个角各剪去一个边长为 $ y $ cm 的小正方形,然后把它折成一个无盖的长方体铁盒。
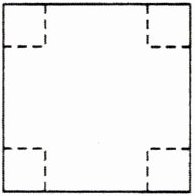
(1) 该铁盒的高是ycm,底面积是______$(x-2y)^{2}$$ cm^2 $；
(2) 将剪下的四个小正方形平铺在铁盒的底面,要求不重叠。当 $ x = 4y $ 时,是否能恰好铺满铁盒底面(不考虑铁皮的厚度)？

答案： 解:
(1)y $(x-2y)^{2}$
(2)当x=4y时,
$(x-2y)^{2}=(4y-2y)^{2}=4y^{2}$,
又四个小正方形的面积为$4y^{2}$,
所以能恰好铺满铁盒底面.

3. 一般情况下 $ \frac{a}{2} + \frac{b}{3} = \frac{a + b}{2 + 3} $ 不成立,但有些数可以使得它成立,例如：$ a = b = 0 $。我们称使得 $ \frac{a}{2} + \frac{b}{3} = \frac{a + b}{2 + 3} $ 成立的一对数 $ a $,$ b $ 为“相伴数对”,记为 $ (a, b) $。
(1) 若 $ (1, b) $ 是“相伴数对”,求 $ b $ 的值；
(2) 写出一个“相伴数对”$ (a, b) $,其中 $ a \neq 0 $,且 $ a \neq 1 $；
(3) 若 $ (m, n) $ 是“相伴数对”,求代数式 $ 3(3m - 2) + 2(2n + 1) $ 的值。

答案： 解:
(1)由$\frac{1}{2}+\frac{b}{3}=\frac{1+b}{2+3}$,可得$b=-\frac{9}{4}$.
(2)可设a=2,则$\frac{2}{2}+\frac{b}{3}=\frac{2+b}{2+3}$,得$b=-\frac{9}{2}$.
所以$(2,-\frac{9}{2})$是“相伴对数”.(答案不唯一)
(3)因为(m,n)是“相伴对数”，
所以有$\frac{m}{2}+\frac{n}{3}=\frac{m+n}{2+3}$,可得9m+4n=0.
原式=9m-6+4n+2=9m+4n-4=-4.