《2025年时代新课程七年级数学上册苏科版》

9. 如图，按要求涂上阴影部分：(1) 将图形甲平移到图形乙；(2) 将图形乙沿图中虚线翻折到图形丙；(3) 将图形丙沿其右下方的顶点旋转$180^{\circ}$到图形丁.

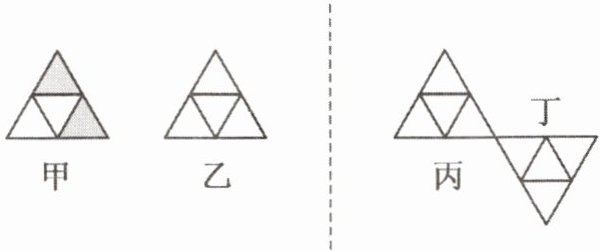
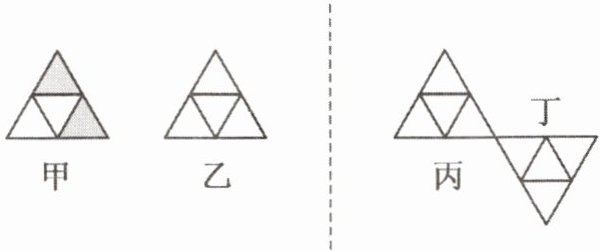
答案：

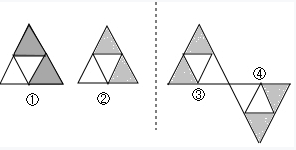
10. 探究：有一长$9cm$，宽$6cm$的长方形纸板，现要求以其一组对边中点所在直线为轴，旋转$180^{\circ}$，得到一个圆柱，现可按照两种方案进行操作：方案一：以较长的一组对边中点所在直线为轴旋转，如图①；方案二：以较短的一组对边中点所在直线为轴旋转，如图②.
(1) 请通过计算说明哪种方案构造的圆柱体积大；
(2) 若将此长方形绕着它的其中一条边所在的直线为轴旋转$360^{\circ}$，则得到的圆柱体积为多少？

答案： 10 解：
(1)方案一：$\pi×(4.5)^{2}×6=121.5\pi(cm^{3})，$
方案二：$\pi×3^{2}×9=81\pi(cm^{3})，$
∵$121.5\pi＞81\pi，$
∴方案一构造的圆柱的体积大；
(2)以较短一条边所在的直线为轴旋转360°，
其体积为：$\pi×9^{2}×6=486\pi(cm^{3})，$
以较长一条边所在的直线为轴旋转360°，
其体积为：$\pi×6^{2}×9=324\pi(cm^{3}).$

11. 如果四张扑克按左图的形式摆放在桌面上，将其中一张旋转$180^{\circ}$后，扑克的放置情况如右图所示，那么旋转的扑克是从左起的(A)


A.第一张
B.第二张
C.第三张
D.第四张

答案： 11 A

12. 将一张长方形的纸片连续平行对折，数一数折痕的条数：对折$1$次，折痕共有1条；对折$2$次，折痕共有3条；对折$5$次，折痕共有31条. 请猜想一下，当对折$n$次时，折痕共有(2^{n}-1)条.

答案： $12 1 3 31 (2^{n}-1)$