《2025年时代新课程七年级数学上册苏科版》

11. （1）计算：$12.6×37+1.26×630$；（2）设$m※n=(m - 1)×(n + 2)$，计算$10※8$的值.

答案： 11.
(1)1260；
(2)90

12. 如图，将两个形状、大小一样的直角三角尺拼成一个四边形，你能拼出多少种形状不同的四边形？画出你所拼出的四边形的示意图.

答案： 能拼出3种形状不同的四边形。
示意图如下（文字描述）：
1. 以一条直角边为公共边拼接，组成平行四边形。
2. 以另一条直角边为公共边拼接，组成平行四边形。
3. 以斜边为公共边拼接，组成平行四边形。
（注：实际答题时需画出对应图形，此处以文字描述示意）

13. (2025春·蕉城区期中)阅读下面材料，并完成相应的任务.
“速算”是指在特定情况下用特定的方法进行计算，它有很强的技巧性. 观察下列各式：$22×28 = 616$；$35×35 = 1225$；$47×43 = 2021$；$51×59 = 3009$；…
我们发现，两位数$ab$与$ac$相乘，当$b + c = 10$时，有如下速算规律：先将十位数字$a$与$a + 1$相乘，得到的结果作为积的前两位数字；再将个位数字$b$和$c$相乘，得到的结果作为积的后两位数字. 如果$b×c$结果是一位数，则在其前面补0.
(1)请根据上述规律计算：$73×77=$5621；$86×84=$7224；
(2)根据上述阅读材料，请你用含字母$a$、$b$、$c$的式子表示这种速算规律.

答案： 13.
(1)5621,7224；
(2)(10a+b)×(10a+c)=100a(a+1)+bc.

14. 将一些数排列成下表形式：

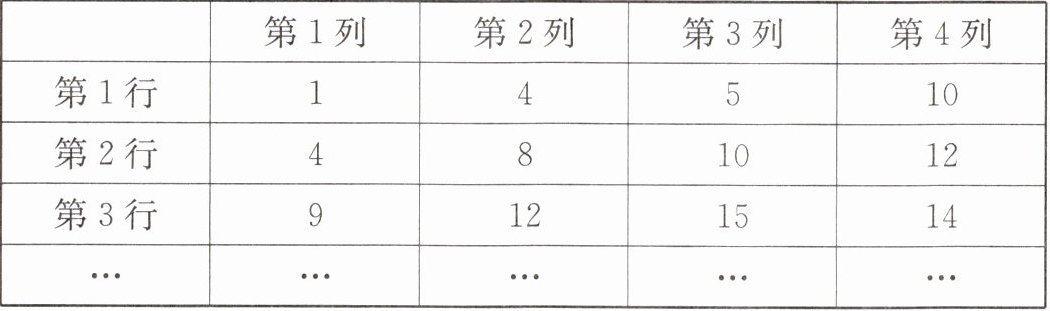
试探索：
（1）第10行第2列的数是多少？
（2）数81所在的行和列分别是多少？
（3）数100所在的行和列分别是多少？

答案： 14.
(1)40；
(2)第9行第1列；
(3)第10行第1列,第25行第2列,第20行第3列,第46行第4列

15. 柳青同学通过学习已经知道：在如图所示的正方形$ABCD$中，如果各边都被三等分，那么图中正方形的总数为$3×3 + 2×2 + 1×1 = 14$. 于是，他把这种计算方法类比到图中长方形$EFGH$中，已知该长方形各边上最短的线段分别相等，于是得出图中正方形的总数为$3×4 + 2×3 + 1×2 = 20$. 你认为他得出的结论正确吗？

答案： 15.结论正确