《2025年时代新课程七年级数学上册苏科版》

11. 某水泥仓库一周 7 天内进出水泥的吨数如下(“+”表示进库,“-”表示出库):+30,-25,-30,+28,-29,-16,-15.
(1) 经过这 7 天,仓库里的水泥是增多还是减少了? 增多或减少了多少吨?
(2) 如果进仓库的水泥装卸费是每吨$a$元,出仓库的水泥装卸费是每吨$b$元,则这 7 天要付多少元装卸费? (用含$a$,$b$的代数式表示)

答案： 11.
(1)减少了，减少了57吨；
(2)58a + 115b.

12. (1) 如图①(单位:cm),用代数式表示出三角尺(涂色部分)的面积;
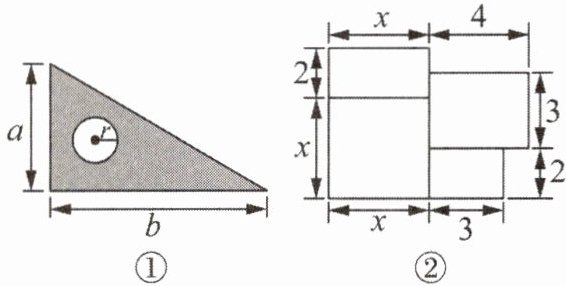
(2) 如图②(单位:m)是一所住宅的建筑平面图,用代数式表示出这所住宅的建筑面积.

答案： $12.(1)(\frac{1}{2}ab - \pi r^{2})cm^{2}；$$(2)(x^{2}+2x + 18)m^{2}.$

13. (2025 春·崇明区期中)某商品打九折后,价格是$a$元,则原价是\frac{a}{0.9}.

答案： $13.\frac{a}{0.9}$

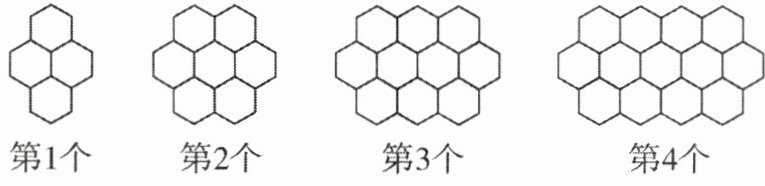
14. 观察下列“蜂窝图”,按照这样的规律,则第$n$个图案中的“ ”的个数是3n + 1.

答案： 14.3n + 1

15. (2024 秋·凉州区月考)有一串代数式:$-x$,$2x^{2}$,$-3x^{3}$,$4x^{4}$,$\cdots$,$-19x^{19}$,$20x^{20}$,$\cdots$,求:
(1) 观察特点,用自己的语言叙述这串代数式的规律;
(2) 写出第 2 025 个代数式;
(3) 写出第$n$个、第$n + 1$个代数式.

答案： 15.
(1)这组单项式的系数和次数都是1开始的连续的整数，且系数第奇数个为负，第偶数个为正；$(2)-2025x^{2025}；$$(3)(-1)^{n}nx^{n},(-1)^{n + 1}(n + 1)x^{n + 1}.$