2025年赢在暑假抢分计划八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在暑假抢分计划八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
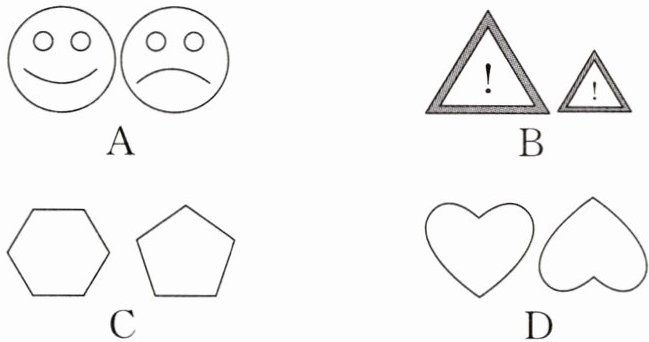
1. 下列各组中的两个图形属于全等图形的是(
D
)
答案:
D
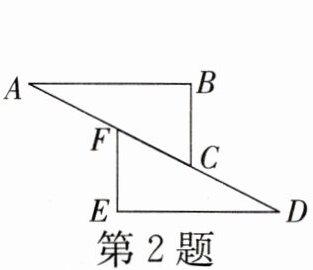
2. 如图,$\triangle ABC \cong \triangle DEF$,若$AC = 5$,$CF = 2$,则$CD$的长为(
A.2
B.2.5
C.3
D.5
C
)
A.2
B.2.5
C.3
D.5
答案:
解:
∵△ABC≌△DEF
∴AC=DF
∵AC=5
∴DF=5
∵DF=CF+CD,CF=2
∴CD=DF-CF=5-2=3
答案:C
∵△ABC≌△DEF
∴AC=DF
∵AC=5
∴DF=5
∵DF=CF+CD,CF=2
∴CD=DF-CF=5-2=3
答案:C
3. 如图,在$\angle AOB$的两边上,分别取$OM = ON$,再分别过点$M$,$N作OA$,$OB$的垂线,交点为$P$,画射线$OP$。可判定$\triangle OMP \cong \triangle ONP$,依据是(
A.ASA
B.SAS
C.AAS
D.HL
D
)A.ASA
B.SAS
C.AAS
D.HL
答案:
解:
∵PM⊥OA,PN⊥OB,
∴∠OMP=∠ONP=90°。
在Rt△OMP和Rt△ONP中,
OM=ON,OP=OP,
∴Rt△OMP≌Rt△ONP(HL)。
D
∵PM⊥OA,PN⊥OB,
∴∠OMP=∠ONP=90°。
在Rt△OMP和Rt△ONP中,
OM=ON,OP=OP,
∴Rt△OMP≌Rt△ONP(HL)。
D
4. 如图,已知$AC = DB$,添加下列条件,仍不能判定$\triangle ABC \cong \triangle DCB$的是(
A.$\angle A = \angle D = 90^{\circ}$
B.$\angle ABC = \angle DCB$
C.$\angle ACB = \angle DBC$
D.$AB = DC$
B
)A.$\angle A = \angle D = 90^{\circ}$
B.$\angle ABC = \angle DCB$
C.$\angle ACB = \angle DBC$
D.$AB = DC$
答案:
解:对于选项A,已知$AC = DB$,$BC = CB$(公共边),$\angle A=\angle D = 90^{\circ}$,根据“HL”可判定$\triangle ABC\cong\triangle DCB$;
对于选项B,已知$AC = DB$,$BC = CB$,$\angle ABC=\angle DCB$,此时是“SSA”,不能判定$\triangle ABC\cong\triangle DCB$;
对于选项C,已知$AC = DB$,$\angle ACB=\angle DBC$,$BC = CB$,根据“SAS”可判定$\triangle ABC\cong\triangle DCB$;
对于选项D,已知$AC = DB$,$AB = DC$,$BC = CB$,根据“SSS”可判定$\triangle ABC\cong\triangle DCB$。
答案:B
对于选项B,已知$AC = DB$,$BC = CB$,$\angle ABC=\angle DCB$,此时是“SSA”,不能判定$\triangle ABC\cong\triangle DCB$;
对于选项C,已知$AC = DB$,$\angle ACB=\angle DBC$,$BC = CB$,根据“SAS”可判定$\triangle ABC\cong\triangle DCB$;
对于选项D,已知$AC = DB$,$AB = DC$,$BC = CB$,根据“SSS”可判定$\triangle ABC\cong\triangle DCB$。
答案:B
5. (扬州)如图,小明家仿古家具的一块三角形状的玻璃坏了,需要重新配一块。小明通过电话给玻璃店老板提供相关数据,为了方便表述,他将该三角形记为$\triangle ABC$,提供下列各组元素的数据,配出来的玻璃不一定符合要求的是(
A.$AB$,$BC$,$CA$
B.$AB$,$BC$,$\angle B$
C.$AB$,$AC$,$\angle B$
D.$\angle A$,$\angle B$,$BC$
C
)A.$AB$,$BC$,$CA$
B.$AB$,$BC$,$\angle B$
C.$AB$,$AC$,$\angle B$
D.$\angle A$,$\angle B$,$BC$
答案:
要判断各组数据能否唯一确定△ABC,需依据三角形全等的判定定理。
选项A:已知AB、BC、CA,即三边对应相等,根据“SSS”(边边边)定理,可唯一确定三角形,符合要求。
- 选项B:已知AB、BC、∠B,即两边及其夹角对应相等,根据“SAS”(边角边)定理,可唯一确定三角形,符合要求。
- 选项C:已知AB、AC、∠B,即两边及其中一边的对角对应相等(SSA),此时可能存在两个不同的三角形满足条件(如锐角三角形和钝角三角形),无法唯一确定,不一定符合要求。
- 选项D:已知∠A、∠B、BC,即两角及其夹边对应相等,根据“ASA”(角边角)定理,可唯一确定三角形,符合要求。
结论:配出来的玻璃不一定符合要求的是C。
答案:C
选项A:已知AB、BC、CA,即三边对应相等,根据“SSS”(边边边)定理,可唯一确定三角形,符合要求。
- 选项B:已知AB、BC、∠B,即两边及其夹角对应相等,根据“SAS”(边角边)定理,可唯一确定三角形,符合要求。
- 选项C:已知AB、AC、∠B,即两边及其中一边的对角对应相等(SSA),此时可能存在两个不同的三角形满足条件(如锐角三角形和钝角三角形),无法唯一确定,不一定符合要求。
- 选项D:已知∠A、∠B、BC,即两角及其夹边对应相等,根据“ASA”(角边角)定理,可唯一确定三角形,符合要求。
结论:配出来的玻璃不一定符合要求的是C。
答案:C
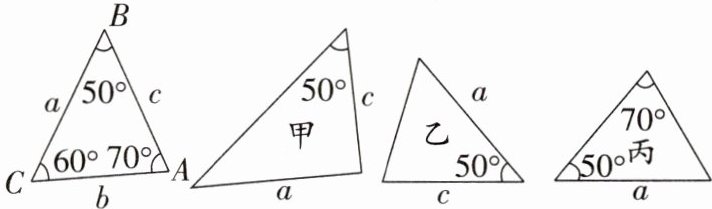
6. 如图,已知$\triangle ABC$的六个元素,则下面甲、乙、丙三个三角形中和$\triangle ABC$全等的图形是(
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
B
) 
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
答案:
解:
- 甲:已知两边(a,c)和其中一边对角(50°),不符合全等判定定理。
- 乙:已知两边(a,c)及其夹角(50°),符合SAS,与△ABC全等。
- 丙:已知两角(50°,70°)和夹边(a),符合ASA,与△ABC全等。
结论:乙和丙与△ABC全等。
B
- 甲:已知两边(a,c)和其中一边对角(50°),不符合全等判定定理。
- 乙:已知两边(a,c)及其夹角(50°),符合SAS,与△ABC全等。
- 丙:已知两角(50°,70°)和夹边(a),符合ASA,与△ABC全等。
结论:乙和丙与△ABC全等。
B
7. 如图,点$A$,$B分别是\angle NOP$,$\angle MOP$平分线上的点,$AB \perp OP于点E$,$BC \perp MN于点C$,$AD \perp MN于点D$,则下列结论错误的是( )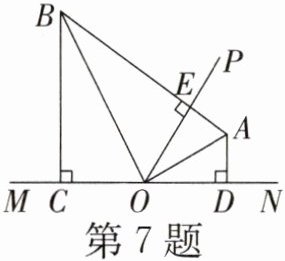
A.$AD + BC = AB$
B.$\angle AOB = 90^{\circ}$
C.与$\angle CBO$互余的角有2个
D.点$O是CD$的中点
C

A.$AD + BC = AB$
B.$\angle AOB = 90^{\circ}$
C.与$\angle CBO$互余的角有2个
D.点$O是CD$的中点
答案:
解:
∵点$A$在$\angle NOP$平分线上,$AD \perp MN$,$AE \perp OP$,
∴$AD = AE$(角平分线性质)。
同理,点$B$在$\angle MOP$平分线上,$BC \perp MN$,$BE \perp OP$,
∴$BC = BE$。
∵$AB = AE + BE$,
∴$AB = AD + BC$,A正确。
∵$OA$平分$\angle NOP$,$OB$平分$\angle MOP$,
∴$\angle AOP = \frac{1}{2}\angle NOP$,$\angle BOP = \frac{1}{2}\angle MOP$。
∵$\angle MOP + \angle NOP = 180^\circ$(平角定义),
∴$\angle AOB = \angle AOP + \angle BOP = \frac{1}{2}(\angle MOP + \angle NOP) = 90^\circ$,B正确。
$\angle CBO + \angle COB = 90^\circ$(直角三角形两锐角互余),
$\angle COB = \angle EOB$(角平分线),$\angle EOB + \angle OAE = 90^\circ$($\angle AOB = 90^\circ$),
$\angle OAE = \angle OAD$(角平分线),
∴与$\angle CBO$互余的角有$\angle COB$、$\angle EOB$、$\angle OAE$、$\angle OAD$,共4个,C错误。
在$Rt\triangle OCB$和$Rt\triangle OEB$中,$\begin{cases} OB=OB \\ BC=BE \end{cases}$,
∴$Rt\triangle OCB \cong Rt\triangle OEB$(HL),
∴$OC = OE$。
同理,$Rt\triangle OEA \cong Rt\triangle ODA$(HL),
∴$OE = OD$,
∴$OC = OD$,即点$O$是$CD$中点,D正确。
结论错误的是C。
答案:C
∵点$A$在$\angle NOP$平分线上,$AD \perp MN$,$AE \perp OP$,
∴$AD = AE$(角平分线性质)。
同理,点$B$在$\angle MOP$平分线上,$BC \perp MN$,$BE \perp OP$,
∴$BC = BE$。
∵$AB = AE + BE$,
∴$AB = AD + BC$,A正确。
∵$OA$平分$\angle NOP$,$OB$平分$\angle MOP$,
∴$\angle AOP = \frac{1}{2}\angle NOP$,$\angle BOP = \frac{1}{2}\angle MOP$。
∵$\angle MOP + \angle NOP = 180^\circ$(平角定义),
∴$\angle AOB = \angle AOP + \angle BOP = \frac{1}{2}(\angle MOP + \angle NOP) = 90^\circ$,B正确。
$\angle CBO + \angle COB = 90^\circ$(直角三角形两锐角互余),
$\angle COB = \angle EOB$(角平分线),$\angle EOB + \angle OAE = 90^\circ$($\angle AOB = 90^\circ$),
$\angle OAE = \angle OAD$(角平分线),
∴与$\angle CBO$互余的角有$\angle COB$、$\angle EOB$、$\angle OAE$、$\angle OAD$,共4个,C错误。
在$Rt\triangle OCB$和$Rt\triangle OEB$中,$\begin{cases} OB=OB \\ BC=BE \end{cases}$,
∴$Rt\triangle OCB \cong Rt\triangle OEB$(HL),
∴$OC = OE$。
同理,$Rt\triangle OEA \cong Rt\triangle ODA$(HL),
∴$OE = OD$,
∴$OC = OD$,即点$O$是$CD$中点,D正确。
结论错误的是C。
答案:C
8. 如图,$AB = 4\ cm$,$\angle A = \angle B = 60^{\circ}$,$AC = BD = 3\ cm$。点$P在线段AB上以1\ cm/s的速度由点A向点B$运动,同时,点$Q在线段BD上以x\ cm/s的速度由点B向点D$运动,它们运动的时间为$t(s)$。当$\triangle ACP与\triangle BPQ$全等时,$x$的值为(
A.1
B.2
C.1或2
D.1或1.5
D
)A.1
B.2
C.1或2
D.1或1.5
答案:
解:由题意得,$AP = t\ cm$,$BP = AB - AP = (4 - t)\ cm$,$BQ = xt\ cm$。
情况一:若$\triangle ACP \cong \triangle BPQ$,则$AC = BP$,$AP = BQ$。
$AC = 3\ cm$,$BP = 4 - t$,$\therefore 3 = 4 - t$,解得$t = 1$。
$AP = t = 1\ cm$,$BQ = xt = x × 1 = x\ cm$,$\therefore 1 = x$,即$x = 1$。
情况二:若$\triangle ACP \cong \triangle BQP$,则$AC = BQ$,$AP = BP$。
$AP = BP$,$AP = t$,$BP = 4 - t$,$\therefore t = 4 - t$,解得$t = 2$。
$AC = 3\ cm$,$BQ = xt = 2x\ cm$,$\therefore 3 = 2x$,解得$x = 1.5$。
综上,$x$的值为$1$或$1.5$。
答案:D
情况一:若$\triangle ACP \cong \triangle BPQ$,则$AC = BP$,$AP = BQ$。
$AC = 3\ cm$,$BP = 4 - t$,$\therefore 3 = 4 - t$,解得$t = 1$。
$AP = t = 1\ cm$,$BQ = xt = x × 1 = x\ cm$,$\therefore 1 = x$,即$x = 1$。
情况二:若$\triangle ACP \cong \triangle BQP$,则$AC = BQ$,$AP = BP$。
$AP = BP$,$AP = t$,$BP = 4 - t$,$\therefore t = 4 - t$,解得$t = 2$。
$AC = 3\ cm$,$BQ = xt = 2x\ cm$,$\therefore 3 = 2x$,解得$x = 1.5$。
综上,$x$的值为$1$或$1.5$。
答案:D
查看更多完整答案,请扫码查看


