2025年赢在暑假抢分计划八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在暑假抢分计划八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
10. 为了考察甲、乙两种小麦的长势,某农研所科技人员,分别从中随机抽取10株麦苗,测得苗高(单位:cm)如下表:
则____种小麦的长势比较整齐.(填“甲”或“乙”)
则____种小麦的长势比较整齐.(填“甲”或“乙”)
答案:
解:计算甲种小麦苗高的平均数:$\overline{x}_{甲}=\frac{1}{10}(12+13+14+15+10+16+13+11+15+11)=13$cm
计算乙种小麦苗高的平均数:$\overline{x}_{乙}=\frac{1}{10}(11+16+17+14+13+19+6+8+10+16)=13$cm
计算甲种小麦苗高的方差:
$s^{2}_{甲}=\frac{1}{10}[(12-13)^{2}+(13-13)^{2}+\cdots+(11-13)^{2}]=3.6$
计算乙种小麦苗高的方差:
$s^{2}_{乙}=\frac{1}{10}[(11-13)^{2}+(16-13)^{2}+\cdots+(16-13)^{2}]=15.8$
因为$s^{2}_{甲}<s^{2}_{乙}$,所以甲种小麦的长势比较整齐。
甲
计算乙种小麦苗高的平均数:$\overline{x}_{乙}=\frac{1}{10}(11+16+17+14+13+19+6+8+10+16)=13$cm
计算甲种小麦苗高的方差:
$s^{2}_{甲}=\frac{1}{10}[(12-13)^{2}+(13-13)^{2}+\cdots+(11-13)^{2}]=3.6$
计算乙种小麦苗高的方差:
$s^{2}_{乙}=\frac{1}{10}[(11-13)^{2}+(16-13)^{2}+\cdots+(16-13)^{2}]=15.8$
因为$s^{2}_{甲}<s^{2}_{乙}$,所以甲种小麦的长势比较整齐。
甲
11. 某班有50人,一次数学测试后,老师对测试成绩进行了统计.由于小明没有参加此次集体测试,因此计算其他49人的平均分为92分,方差$s_{1}^{2}= 5$.后来小明进行了补测,成绩是92分,则该班50人的数学测试成绩的方差$s_{2}^{2}= $
4.9
.
答案:
解:49人的总分为$49×92 = 4508$分,
50人的总分为$4508 + 92 = 4600$分,
50人的平均分为$4600÷50 = 92$分,
设49人的成绩分别为$x_{1},x_{2},\cdots,x_{49}$,则$\frac{1}{49}[(x_{1}-92)^{2}+(x_{2}-92)^{2}+\cdots+(x_{49}-92)^{2}]=5$,
所以$(x_{1}-92)^{2}+(x_{2}-92)^{2}+\cdots+(x_{49}-92)^{2}=49×5 = 245$,
50人的方差$s_{2}^{2}=\frac{1}{50}[245+(92 - 92)^{2}]=\frac{245}{50}=4.9$。
4.9
50人的总分为$4508 + 92 = 4600$分,
50人的平均分为$4600÷50 = 92$分,
设49人的成绩分别为$x_{1},x_{2},\cdots,x_{49}$,则$\frac{1}{49}[(x_{1}-92)^{2}+(x_{2}-92)^{2}+\cdots+(x_{49}-92)^{2}]=5$,
所以$(x_{1}-92)^{2}+(x_{2}-92)^{2}+\cdots+(x_{49}-92)^{2}=49×5 = 245$,
50人的方差$s_{2}^{2}=\frac{1}{50}[245+(92 - 92)^{2}]=\frac{245}{50}=4.9$。
4.9
12. (牡丹江)甲乙两班举行一分钟跳绳比赛,参赛学生每分钟跳绳次数的统计结果如下表:
某同学分析上表后得到如下结论:①甲、乙两班学生平均成绩相同;②乙班优秀人数多于甲班优秀人数(每分钟跳绳≥110次为优秀);③甲班成绩的波动比乙班大.则正确结论的序号是
某同学分析上表后得到如下结论:①甲、乙两班学生平均成绩相同;②乙班优秀人数多于甲班优秀人数(每分钟跳绳≥110次为优秀);③甲班成绩的波动比乙班大.则正确结论的序号是
①②③
.
答案:
解:①甲、乙两班学生平均成绩相同;②乙班优秀人数多于甲班优秀人数;③甲班成绩的波动比乙班大.则正确结论的序号是①②③.
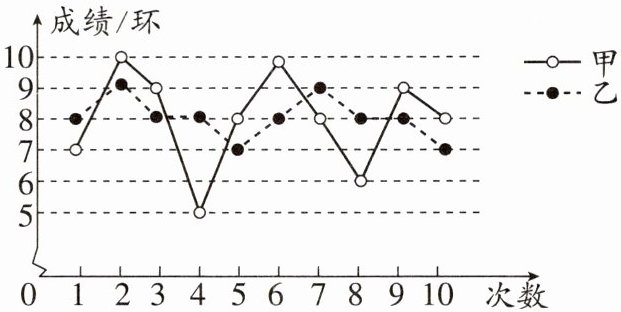
13. (12分)要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲、乙这10次射击成绩的方差$s_{甲}^{2},s_{乙}^{2}$哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选____参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选____参赛更合适.
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲、乙这10次射击成绩的方差$s_{甲}^{2},s_{乙}^{2}$哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选____参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选____参赛更合适.

答案:
13.
(1)解:$\overline{x}_{乙}=(8+9+8+8+7+8+9+8+8+7)÷10=8$(环);
(2)$s_{甲}^{2}>s_{乙}^{2}$;
(3)乙;甲
(1)解:$\overline{x}_{乙}=(8+9+8+8+7+8+9+8+8+7)÷10=8$(环);
(2)$s_{甲}^{2}>s_{乙}^{2}$;
(3)乙;甲
14. (12分)甲、乙在5次打靶测试中命中环数如下:
甲:8,8,7,8,9;
乙:5,9,7,10,9.
(1)填写下表:

(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差____.(填“变大”“变小”或“不变”).
甲:8,8,7,8,9;
乙:5,9,7,10,9.
(1)填写下表:

(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差____.(填“变大”“变小”或“不变”).
答案:
14.
(1)8;8;9;
(2)解:甲、乙平均成绩相等,甲的方差小,发挥更稳定,故选择甲;
(3)变小
(1)8;8;9;
(2)解:甲、乙平均成绩相等,甲的方差小,发挥更稳定,故选择甲;
(3)变小
15. (14分)(宁夏)宁夏某枸杞育种改良试验基地对新培育的甲、乙两个品种各试种一亩,从两块试验地中各随机抽取10棵,对其产量(千克/棵)进行整理分析.下面给出了部分信息:
甲品种:2.0,3.2,3.1,3.2,3.1,2.5,3.2,3.6,3.8,3.9
乙品种:如图所示
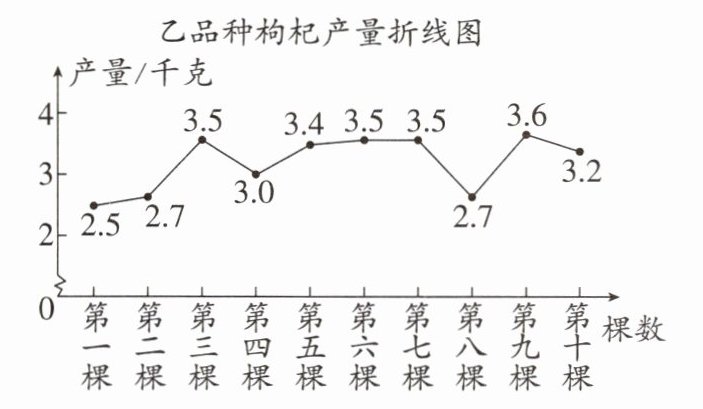
根据以上信息,完成下列问题:
(1)填空:$a= $____,$b= $____;
(2)若乙品种种植300棵,估计其产量不低于3.16千克的棵数;
(3)请从某一个方面简要说明哪个品种更好.
甲品种:2.0,3.2,3.1,3.2,3.1,2.5,3.2,3.6,3.8,3.9
乙品种:如图所示

根据以上信息,完成下列问题:
(1)填空:$a= $____,$b= $____;
(2)若乙品种种植300棵,估计其产量不低于3.16千克的棵数;
(3)请从某一个方面简要说明哪个品种更好.
答案:
15.
(1)3.2;3.5;
(2)解:$300×\frac{6}{10}=180$(棵);
(3)解:甲、乙平均产量相等,乙品种方差更小,产量更稳定,故乙品种更好.
(1)3.2;3.5;
(2)解:$300×\frac{6}{10}=180$(棵);
(3)解:甲、乙平均产量相等,乙品种方差更小,产量更稳定,故乙品种更好.
16. (14分)(通辽)某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
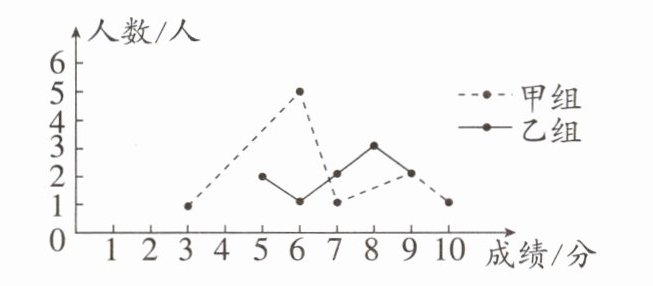
(1)求出成绩统计分析表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
见此图标微信扫码 暑期同步练,学透知识点!

(1)求出成绩统计分析表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
见此图标微信扫码 暑期同步练,学透知识点!
答案:
16.
(1)解:$a=6$;$b=\frac{5×2+6×1+7×2+8×3+9×2}{10}=7.2$;
(2)甲组;
(3)①乙组平均分高于甲组;②乙组方差小于甲组,成绩更稳定.
(1)解:$a=6$;$b=\frac{5×2+6×1+7×2+8×3+9×2}{10}=7.2$;
(2)甲组;
(3)①乙组平均分高于甲组;②乙组方差小于甲组,成绩更稳定.
查看更多完整答案,请扫码查看


