《2025年赢在暑假抢分计划八年级数学人教版》

1.(凉山州)下列长度的三条线段能组成三角形的是(C)
A.3,4,8
B.5,6,11
C.5,6,10
D.5,5,10

答案： 解：A. 3+4=7＜8，不能组成三角形；
B. 5+6=11，不能组成三角形；
C. 5+6=11＞10，6-5=1＜10，能组成三角形；
D. 5+5=10，不能组成三角形。
结论：C

2. 能把一个三角形分成两个面积相等的三角形的线段是三角形的(A)
A.中线
B.高线
C.角平分线
D.无法确定

答案： 解：三角形的中线将三角形分成两个等底同高的三角形，根据三角形面积公式$S = \frac{1}{2}ah$（$a$为底，$h$为高），这两个三角形面积相等。
答案：A

3. 下列说法中,正确的是(C)
A.等腰三角形是等边三角形
B.三角形按边分类可分为等腰三角形、等边三角形和三边都不相等的三角形
C.三角形按角分类可分为锐角三角形、直角三角形和钝角三角形
D.三角形的两边之差大于第三边

答案： C

4. 具备下列条件的△ABC中,不是直角三角形的是(D)
A.∠A= 26°,∠B= 64°
B.∠A-∠B= ∠C
C.∠B= 90°-∠A
D.∠A：∠B：∠C= 2：3：4

答案： A. ∠A+∠B=26°+64°=90°，则∠C=90°，是直角三角形；
B. ∠A-∠B=∠C，又∠A+∠B+∠C=180°，得∠A=90°，是直角三角形；
C. ∠B=90°-∠A，得∠A+∠B=90°，∠C=90°，是直角三角形；
D. 设∠A=2x，∠B=3x，∠C=4x，2x+3x+4x=180°，x=20°，∠C=80°，不是直角三角形。
答案：D

5.(通辽)正多边形的每个内角为108°,则它的边数是(D)
A.4
B.6
C.7
D.5

答案： 解：设该正多边形的边数为$n$。
因为正多边形的内角和公式为$(n - 2)×180°$，且每个内角为$108°$，所以可得方程：
$\frac{(n - 2)×180°}{n} = 108°$
$(n - 2)×180 = 108n$
$180n - 360 = 108n$
$180n - 108n = 360$
$72n = 360$
$n = 5$
答案：D

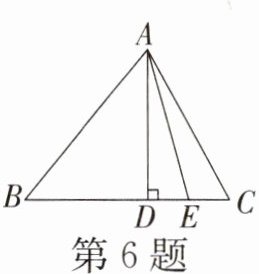
6. 如图,在△ABC中,AD⊥BC于点D,则图中以AD为高的三角形有(D)

A.3个
B.4个
C.5个
D.6个

答案： 解：图中以AD为高的三角形有：△ABC、△ABD、△ABE、△ADE、△ADC、△AEC，共6个。
答案：D

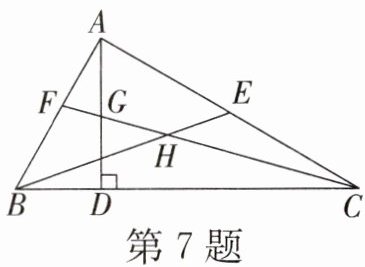
7. 如图,在△ABC中,∠BAC= 90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是(C)
①$S_{\triangle ABE}$的面积= $S_{\triangle BCE}$的面积；②∠AFG= ∠AGF；③∠FAG= 2∠ACF；④AF= FB。

A.①②③④
B.①②④
C.①②③
D.③④

答案： 解：①
∵BE是中线，
∴AE=CE，
∵△ABE和△BCE等底同高，
∴S△ABE=S△BCE，①正确；
②
∵∠BAC=90°，AD是高，
∴∠BAD+∠CAD=90°，∠CAD+∠ACD=90°，
∴∠BAD=∠ACD，
∵CF是角平分线，
∴∠ACF=∠BCF，
∵∠AFG=∠BAD+∠BCF，∠AGF=∠CAD+∠ACF，
∴∠AFG=∠AGF，②正确；
③
∵∠BAC=90°，AD是高，
∴∠FAG=∠ABC，
∵CF是角平分线，
∴∠ACF=∠BCD=1/2∠ACB，
∵∠ABC+∠ACB=90°，
∴∠FAG=90°-∠ACB=90°-2∠ACF，③错误；
④
∵CF是角平分线，只有当∠ABC=∠ACB时，AF=FB，④错误。
综上，正确的是①②③，答案选C。

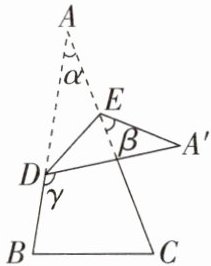
8. 如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的点A'处,折痕为DE。如果∠A= α,∠CEA'= β,∠BDA'= γ,那么下列式子中正确的是( A )

A.γ= 2α+β
B.γ= α+2β
C.γ= α+β
D.γ= 180°-α-β

答案： 解：设DA'与AC交于点F。
由折叠性质得∠A=∠A'=α。
在△A'EF中，∠A'FE=∠CEA'+∠A'=β+α。
∠DFC=∠A'FE=α+β（对顶角相等）。
在△DFC中，∠BDA'=∠A+∠DFC=α+(α+β)=2α+β。
即γ=2α+β。
答案：A

9. 如图,人字梯中间一般会设计一个“拉杆”,这样做的依据是三角形具有稳定性。

答案： 三角形具有稳定性

10. 一个等腰三角形的周长是18,一边长为4,则它的腰长为7。

答案： 解：
情况一：若腰长为4，则底边长为18 - 4 - 4 = 10。
因为4 + 4 = 8 ＜ 10，不满足三角形两边之和大于第三边，所以此情况不成立。
情况二：若底边长为4，则腰长为(18 - 4)÷2 = 7。
因为7 + 7 = 14 ＞ 4，7 + 4 = 11 ＞ 7，满足三角形两边之和大于第三边，所以此情况成立。
7