《2025年赢在暑假抢分计划八年级数学人教版》

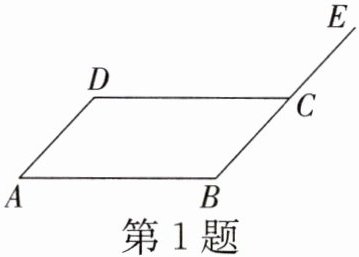
1. (弥勒市校级月考)如图,$E为□ ABCD的边BC$的延长线上一点,若$\angle DCE = 128^{\circ}$,则$\angle A$的度数为(C)

A.$32^{\circ}$
B.$42^{\circ}$
C.$52^{\circ}$
D.$62^{\circ}$

答案： 解：
∵四边形ABCD是平行四边形，
∴AD//BC，∠A=∠BCD。
∵∠DCE=128°，∠BCD+∠DCE=180°，
∴∠BCD=180°-∠DCE=180°-128°=52°。
∴∠A=∠BCD=52°。
答案：C

2. (招远市期末)如图,$□ ABCD的周长为30\mathrm{cm}$,$\triangle ABC的周长为27\mathrm{cm}$,则对角线$AC$的长为(C)

A.$27\mathrm{cm}$
B.$17\mathrm{cm}$
C.$12\mathrm{cm}$
D.$10\mathrm{cm}$

答案： 解：
∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC。
∵□ABCD的周长为30cm，
∴AB+BC+CD+AD=30cm，
∴2(AB+BC)=30cm，
∴AB+BC=15cm。
∵△ABC的周长为27cm，
∴AB+BC+AC=27cm，
∴AC=27cm-(AB+BC)=27cm-15cm=12cm。
答案：C

3. (河北)依据所标数据,下列一定为平行四边形的是(D)

答案： D

4. (沈阳)如图,在$\mathrm{Rt}\triangle ABC$中,$\angle A = 30^{\circ}$,点$D$,$E分别是直角边AC$,$BC$的中点,连接$DE$,则$\angle CED$的度数是(B)

A.$70^{\circ}$
B.$60^{\circ}$
C.$30^{\circ}$
D.$20^{\circ}$

答案： 解：在$\mathrm{Rt}\triangle ABC$中，$\angle C=90^{\circ}$，$\angle A=30^{\circ}$，
$\therefore \angle B=60^{\circ}$。
$\because D$，$E$分别是$AC$，$BC$的中点，
$\therefore DE$是$\triangle ABC$的中位线，
$\therefore DE// AB$，
$\therefore \angle CED=\angle B=60^{\circ}$。
答案：B

5. 如图,四边形$ABCD的对角线相交于点O$,且$AO = CO$,那么下列条件中不能判断四边形$ABCD$为平行四边形的是(C)
A.$OB = OD$
B.$AB// CD$
C.$AB = CD$
D.$\angle ADB = \angle DBC$

答案： 解：
A. 对角线互相平分的四边形是平行四边形，$AO=CO$且$OB=OD$，能判断，不符合题意。
B. $AB// CD$，则$\angle OAB=\angle OCD$，$\angle OBA=\angle ODC$，又$AO=CO$，可证$\triangle AOB≌\triangle COD(AAS)$，得$OB=OD$，能判断，不符合题意。
C. $AB=CD$，仅一组对边相等，不能判断四边形$ABCD$为平行四边形，符合题意。
D. $\angle ADB=\angle DBC$，则$AD// BC$，同理可证$\triangle AOD≌\triangle COB(AAS)$，得$OB=OD$，能判断，不符合题意。
答案：C

6. (嘉兴)如图,在$\triangle ABC$中,$AB = AC = 8$,点$E$,$F$,$G分别在边AB$,$BC$,$AC$上,$EF// AC$,$GF// AB$,则四边形$AEFG$的周长是(B)
A.8
B.16
C.24
D.32

答案： 解：
∵EF//AC，GF//AB，
∴四边形AEFG是平行四边形，
∴AE=GF，AG=EF。
∵AB=AC=8，
∴∠B=∠C。
∵EF//AC，
∴∠EFB=∠C=∠B，
∴EB=EF。
同理，FC=GF=AE。
设AE=x，则EB=AB-AE=8-x，
∴EF=EB=8-x。
四边形AEFG的周长=2(AE+EF)=2(x+8-x)=16。
答案：B

7. (惠济区校级期末)如图,在$\mathrm{Rt}\triangle ABC$中,$\angle B = 90^{\circ}$,$BC = 4$,$AC = 5$,点$D在边BC$上,以$AC为对角线的所有平行四边形ADCE$中,$DE$的最小值是(A)
A.3
B.6
C.8
D.10

答案： 解：在Rt△ABC中，∠B=90°，BC=4，AC=5，
由勾股定理得：AB=$\sqrt{AC^2-BC^2}=\sqrt{5^2-4^2}=3$。
∵四边形ADCE是平行四边形，
∴O为AC中点，OD=OE=$\frac{1}{2}$DE，
∴DE=2OD，当OD最小时，DE最小。
∵点D在BC上，OD⊥BC时OD最小，
又
∵∠B=90°，AB⊥BC，
∴OD//AB，O为AC中点，
∴OD是△ABC中位线，OD=$\frac{1}{2}$AB=$\frac{3}{2}$，
∴DE=2OD=3。
答案：A

8. (河口区期末)如图,$EF过□ ABCD对角线的交点O$,交$AD于点E$,交$BC于点F$,则：①$OE = OF$；②图中共有4对全等三角形；③若$AB = 4$,$AC = 6$,则$2 ＜ BD ＜ 14$；④$S_{\text{四边形}ABFE} = S_{\triangle ABC}$.其中正确的结论有(C)

A.①④

B.①②④
C.①③④
D.①②③

答案： 解：①
∵四边形ABCD是平行四边形，
∴AD//BC，OA=OC，
∴∠OAE=∠OCF，∠OEA=∠OFC，
在△AOE和△COF中，
$\left\{\begin{array}{l} ∠OAE=∠OCF\\ ∠OEA=∠OFC\\ OA=OC\end{array}\right.$，
∴△AOE≌△COF(AAS)，
∴OE=OF，①正确；
②图中全等三角形有：△ABC≌△CDA，△ABD≌△CDB，△AOB≌△COD，△AOD≌△COB，△AOE≌△COF，△DOE≌△BOF，共6对，②错误；
③
∵四边形ABCD是平行四边形，AC=6，
∴OA=OC=3，
在△AOB中，AB=4，OA=3，
∴4-3＜OB＜4+3，即1＜OB＜7，
∵BD=2OB，
∴2＜BD＜14，③正确；
④
∵△AOE≌△COF，
∴S_△AOE=S_△COF，
∵S_{四边形ABFE}=S_△ABC-S_△COF+S_△AOE=S_△ABC，④正确。
综上，正确的结论有①③④，答案选C。