2025年赢在暑假抢分计划八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在暑假抢分计划八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
9. 已知一组数据$a_{1},a_{2},a_{3},a_{4},a_{5}$的平均数为8,则另一组数据$a_{1}+10,a_{2}-10,a_{3}+10,a_{4}-10,a_{5}+10$的平均数是____
10
.
答案:
解:因为数据$a_{1},a_{2},a_{3},a_{4},a_{5}$的平均数为8,所以$\frac{a_{1}+a_{2}+a_{3}+a_{4}+a_{5}}{5}=8$,即$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=40$。
新数据的总和为$(a_{1}+10)+(a_{2}-10)+(a_{3}+10)+(a_{4}-10)+(a_{5}+10)$
$=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+(10 - 10 + 10 - 10 + 10)$
$=40 + 10 = 50$。
新数据的平均数为$\frac{50}{5}=10$。
10
新数据的总和为$(a_{1}+10)+(a_{2}-10)+(a_{3}+10)+(a_{4}-10)+(a_{5}+10)$
$=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+(10 - 10 + 10 - 10 + 10)$
$=40 + 10 = 50$。
新数据的平均数为$\frac{50}{5}=10$。
10
10. (青岛)小明参加“建团百年,我为团旗添光彩”主题演讲比赛,其演讲形象、内容、效果三项分别是9分、8分、8分.若将三项得分依次按3:4:3的比例确定最终成绩,则小明的最终比赛成绩为
8.3
分.
答案:
解:根据题意,计算加权平均数。
$\begin{aligned}\text{最终成绩}&=\frac{9×3 + 8×4 + 8×3}{3 + 4 + 3}\\&=\frac{27 + 32 + 24}{10}\\&=\frac{83}{10}\\&=8.3\end{aligned}$
8.3
$\begin{aligned}\text{最终成绩}&=\frac{9×3 + 8×4 + 8×3}{3 + 4 + 3}\\&=\frac{27 + 32 + 24}{10}\\&=\frac{83}{10}\\&=8.3\end{aligned}$
8.3
11. 自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么,所有满足条件的x,y中,$x+y$的最大值是____.
5
答案:
解:将自然数4,5,5,x,y从小到大排列后,数据共有5个数,中位数是第3个数,已知中位数为4,所以第3个数是4,因此这组数据排列后为:a,b,4,c,d(a,b,c,d为x,y,4,5,5中的数)。
因为唯一的众数是5,所以5出现的次数最多且唯一,5已经出现2次,所以4出现的次数不能超过2次,且其他数出现次数不能等于2次。
由于中位数是4,所以至少有两个数小于或等于4,又因为5是唯一众数,所以x,y不能同时为5,且x,y中最多有一个4(若有两个4,则4和5都是众数,不满足唯一众数)。
要使x,y为自然数且满足排列后中位数为4,x,y只能是小于或等于4的自然数,且不能出现两个相同的非5的数(除5外)。
可能的x,y取值(x≤y):
- 当x=0,y=3时,排列为0,3,4,5,5,满足条件;
- 当x=0,y=4时,排列为0,4,4,5,5,此时4和5都是众数,不满足;
- 当x=1,y=2时,排列为1,2,4,5,5,满足条件;
- 当x=1,y=3时,排列为1,3,4,5,5,满足条件;
- 当x=1,y=4时,排列为1,4,4,5,5,众数不唯一,不满足;
- 当x=2,y=2时,排列为2,2,4,5,5,众数不唯一,不满足;
- 当x=2,y=3时,排列为2,3,4,5,5,满足条件;
- 当x=2,y=4时,排列为2,4,4,5,5,众数不唯一,不满足;
- 当x=3,y=3时,排列为3,3,4,5,5,众数不唯一,不满足;
- 当x=3,y=4时,排列为3,4,4,5,5,众数不唯一,不满足;
- 当x=4,y=4时,排列为4,4,4,5,5,众数不唯一,不满足。
满足条件的x,y组合中,x+y的最大值为1+3=4,2+3=5,0+3=3,1+2=3,所以最大值为5。
5
因为唯一的众数是5,所以5出现的次数最多且唯一,5已经出现2次,所以4出现的次数不能超过2次,且其他数出现次数不能等于2次。
由于中位数是4,所以至少有两个数小于或等于4,又因为5是唯一众数,所以x,y不能同时为5,且x,y中最多有一个4(若有两个4,则4和5都是众数,不满足唯一众数)。
要使x,y为自然数且满足排列后中位数为4,x,y只能是小于或等于4的自然数,且不能出现两个相同的非5的数(除5外)。
可能的x,y取值(x≤y):
- 当x=0,y=3时,排列为0,3,4,5,5,满足条件;
- 当x=0,y=4时,排列为0,4,4,5,5,此时4和5都是众数,不满足;
- 当x=1,y=2时,排列为1,2,4,5,5,满足条件;
- 当x=1,y=3时,排列为1,3,4,5,5,满足条件;
- 当x=1,y=4时,排列为1,4,4,5,5,众数不唯一,不满足;
- 当x=2,y=2时,排列为2,2,4,5,5,众数不唯一,不满足;
- 当x=2,y=3时,排列为2,3,4,5,5,满足条件;
- 当x=2,y=4时,排列为2,4,4,5,5,众数不唯一,不满足;
- 当x=3,y=3时,排列为3,3,4,5,5,众数不唯一,不满足;
- 当x=3,y=4时,排列为3,4,4,5,5,众数不唯一,不满足;
- 当x=4,y=4时,排列为4,4,4,5,5,众数不唯一,不满足。
满足条件的x,y组合中,x+y的最大值为1+3=4,2+3=5,0+3=3,1+2=3,所以最大值为5。
5
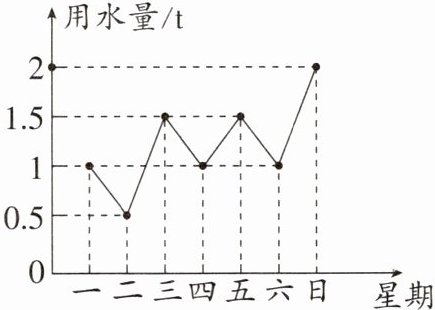
12. (台山市校级一模)小王统计了一周家庭用水量,绘制了如图的统计图,那么这周用水量的众数是
1
,中位数是1
.
答案:
解:由统计图可知,一周各天用水量(单位:t)分别为:1,0.5,1.5,1,1.5,1,2。
将数据从小到大排列:0.5,1,1,1,1.5,1.5,2。
众数是出现次数最多的数,1出现了3次,次数最多,故众数是1。
中位数是按顺序排列后的第4个数,为1,故中位数是1。
1;1
将数据从小到大排列:0.5,1,1,1,1.5,1.5,2。
众数是出现次数最多的数,1出现了3次,次数最多,故众数是1。
中位数是按顺序排列后的第4个数,为1,故中位数是1。
1;1
13. 某瓜农采用大棚栽培技术种植了一亩地的良种西瓜,这亩地产西瓜600个,在西瓜上市前该瓜农随机摘下了10个成熟的西瓜,称重如下:
|西瓜质量(单位:千克)|5.5|5.4|5.0|4.9|4.6|4.3|
|西瓜个数(单位:个)|1|2|3|2|1|1|
则这10个西瓜的平均质量是
|西瓜质量(单位:千克)|5.5|5.4|5.0|4.9|4.6|4.3|
|西瓜个数(单位:个)|1|2|3|2|1|1|
则这10个西瓜的平均质量是
5
千克,根据计算结果你估计这亩地的西瓜产量约是3000
千克.
答案:
解:这10个西瓜的总质量为:
$5.5×1 + 5.4×2 + 5.0×3 + 4.9×2 + 4.6×1 + 4.3×1$
$=5.5 + 10.8 + 15.0 + 9.8 + 4.6 + 4.3$
$=50$(千克)
平均质量为:$50÷10 = 5$(千克)
估计这亩地的西瓜产量约是:$600×5 = 3000$(千克)
5;3000
$5.5×1 + 5.4×2 + 5.0×3 + 4.9×2 + 4.6×1 + 4.3×1$
$=5.5 + 10.8 + 15.0 + 9.8 + 4.6 + 4.3$
$=50$(千克)
平均质量为:$50÷10 = 5$(千克)
估计这亩地的西瓜产量约是:$600×5 = 3000$(千克)
5;3000
14. 如下是抽查的某班10名同学中考体育测试成绩统计表.
|成绩(分)|30|25|20|15|
|人数(人)|2|x|y|1|
若成绩的平均数为23,中位数是a,众数是b,则$a-b$的值是____
|成绩(分)|30|25|20|15|
|人数(人)|2|x|y|1|
若成绩的平均数为23,中位数是a,众数是b,则$a-b$的值是____
2.5
.
答案:
解:根据题意,得
$\begin{cases}2 + x + y + 1 = 10 \\frac{30 × 2 + 25x + 20y + 15 × 1}{10} = 23\end{cases}$
解得
$\begin{cases}x = 3 \\y = 4\end{cases}$
10名同学成绩按从小到大排列为:15,20,20,20,20,25,25,25,30,30
中位数$a = \frac{20 + 25}{2} = 22.5$
众数$b = 20$
$a - b = 22.5 - 20 = 2.5$
2.5
$\begin{cases}2 + x + y + 1 = 10 \\frac{30 × 2 + 25x + 20y + 15 × 1}{10} = 23\end{cases}$
解得
$\begin{cases}x = 3 \\y = 4\end{cases}$
10名同学成绩按从小到大排列为:15,20,20,20,20,25,25,25,30,30
中位数$a = \frac{20 + 25}{2} = 22.5$
众数$b = 20$
$a - b = 22.5 - 20 = 2.5$
2.5
15. (12分)(杭州)某校学生会要在甲、乙两位候选人中选择一人担任文艺部干事,根据对他们的文化水平、艺术水平、组织能力的测试的综合成绩,进行择优录取,他们的各项成绩(单项满分100分)如下表所示:
|候选人|文化水平|艺术水平|组织能力|
|甲|80分|87分|82分|
|乙|80分|96分|76分|
(1)如果把各项成绩的平均数作为综合成绩,应该录取谁?
(2)如果想录取一名组织能力较强的候选人,把文化水平、艺术水平、组织能力三项成绩分别按照20%,20%,60%的比例计入综合成绩,应该录取谁?
|候选人|文化水平|艺术水平|组织能力|
|甲|80分|87分|82分|
|乙|80分|96分|76分|
(1)如果把各项成绩的平均数作为综合成绩,应该录取谁?
(2)如果想录取一名组织能力较强的候选人,把文化水平、艺术水平、组织能力三项成绩分别按照20%,20%,60%的比例计入综合成绩,应该录取谁?
答案:
(1)甲的平均成绩为$\frac{80 + 87 + 82}{3}=83$(分),乙的平均成绩为$\frac{80 + 96 + 76}{3}=84$(分),因为$84>83$,所以应该录取乙;
(2)甲的综合成绩为$80×20\% + 87×20\% + 82×60\% = 82.6$(分),乙的综合成绩为$80×20\% + 96×20\% + 76×60\% = 80.8$(分),因为$82.6>80.8$,所以应该录取甲。
(1)甲的平均成绩为$\frac{80 + 87 + 82}{3}=83$(分),乙的平均成绩为$\frac{80 + 96 + 76}{3}=84$(分),因为$84>83$,所以应该录取乙;
(2)甲的综合成绩为$80×20\% + 87×20\% + 82×60\% = 82.6$(分),乙的综合成绩为$80×20\% + 96×20\% + 76×60\% = 80.8$(分),因为$82.6>80.8$,所以应该录取甲。
16. (12分)在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140,146,143,175,125,164,134,155,152,168,162,148.
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据的中位数,推断他的成绩如何.
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据的中位数,推断他的成绩如何.
答案:
(1)解:将样本数据从小到大排列:125,134,140,143,146,148,152,155,162,164,168,175。
中位数:$\frac{148 + 152}{2} = 150$。
平均数:$\frac{125 + 134 + 140 + 143 + 146 + 148 + 152 + 155 + 162 + 164 + 168 + 175}{12} = 151$。
(2)解:由
(1)知中位数为150,该选手成绩147分钟快于中位数,推断他的成绩比一半以上选手好。
(1)解:将样本数据从小到大排列:125,134,140,143,146,148,152,155,162,164,168,175。
中位数:$\frac{148 + 152}{2} = 150$。
平均数:$\frac{125 + 134 + 140 + 143 + 146 + 148 + 152 + 155 + 162 + 164 + 168 + 175}{12} = 151$。
(2)解:由
(1)知中位数为150,该选手成绩147分钟快于中位数,推断他的成绩比一半以上选手好。
查看更多完整答案,请扫码查看


