《2025年赢在暑假抢分计划八年级数学人教版》

9. 设地面气温是20℃,如果每升高1km,气温下降6℃,则气温t(℃)与高度h(km)的关系是$t = 20 - 6h$,其中常量是$-6$，$20$,变量是$t$，$h$,$t$是$h$的函数.

答案： $t = 20 - 6h$；$-6$，$20$；$t$，$h$；$t$，$h$

10. (哈尔滨)在函数y = $\frac{x}{5x + 3}$中,自变量x的取值范围是$x \neq -\frac{3}{5}$.

答案： 要使函数$y = \frac{x}{5x + 3}$有意义，分母不能为$0$，即：
$5x + 3 \neq 0$
解得：
$5x \neq -3$
$x \neq -\frac{3}{5}$
故自变量$x$的取值范围是$x \neq -\frac{3}{5}$。
答案：$x \neq -\frac{3}{5}$

11. 已知正比例函数y = kx(k≠0)的图象经过点(-6,2),那么函数值y随自变量x的值的增大而减小.(填“增大”或“减小”)

答案： 解：将点(-6,2)代入y=kx，得2=-6k，解得k=-$\frac{1}{3}$。因为k=-$\frac{1}{3}$＜0，所以函数值y随自变量x的值的增大而减小。
减小

12. 根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是-1.

答案： 解：输入x=7，因为7≥3，所以代入y=(5-x)/2，得y=(5-7)/2=(-2)/2=-1。
输出y的值是-1。

13. 已知直线y = (2 - 3m)x经过点$A(x_1,y_1),B(x_2,y_2),$当$x_1＜x_2$时,有$y_1＞y_2,$则m的取值范围是$m＞\frac{2}{3}$.

答案： 解：
∵当$x_1＜x_2$时，$y_1＞y_2$，
∴直线$y=(2 - 3m)x$中，$y$随$x$的增大而减小，
∴$2 - 3m＜0$，
解得$m＞\frac{2}{3}$。
$m＞\frac{2}{3}$

14. (苏州)一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量y(升)与时间x(分钟)之间的函数关系如图所示,则图中a的值为______.

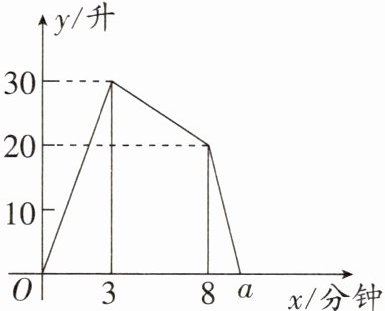
$\frac{29}{3}$

答案： 解：进水管注水速度：$30÷3 = 10$（升/分钟）。
设出水管排水速度为$v$升/分钟。
$3$分钟到$8$分钟共$5$分钟，此时水量从$30$升变为$20$升，可得：$30 + 5×(10 - v)=20$，解得$v = 12$。
$8$分钟后仅出水管排水，水量$20$升，排水时间为$20÷12=\frac{5}{3}$分钟。
$a=8+\frac{5}{3}=\frac{29}{3}$。
$\frac{29}{3}$

15. (9分)写出下列各题中y关于x的函数关系式,并判断y是否为x的正比例函数.
(1)刚上市时西瓜每千克3.6元,买西瓜的总价y元与所买西瓜x千克之间的关系;
(2)仓库内有粉笔400盒,如果每个星期领出36盒,仓库内余下的粉笔盒数y与星期数x之间的关系;
(3)小林的爸爸为小林存了一份教育储蓄,首次存入10000元,以后每个月存入500元,存入总数y元与月数x之间的关系.

答案： 解：
(1)依题意，得 $ y = 3.6x $，$ y $ 是 $ x $ 的正比例函数；
(2)依题意，得 $ y = 400 - 36x $，$ y $ 不是 $ x $ 的正比例函数；
(3)依题意，得 $ y = 10000 + 500x $，$ y $ 不是 $ x $ 的正比例函数.

16. (9分)已知正比例函数y = (2m + 4)x.求:
(1)m为何值时,函数图象经过第一、三象限;
(2)m为何值时,y随x的增大而减小;
(3)m为何值时,点(1,3)在该函数图象上.

答案： 解：
(1)由题意，得$2m + 4＞0$，解得$m＞-2$；
(2)由题意，得$2m + 4＜0$，解得$m＜-2$；
(3)
∵点$(1,3)$在该函数图象上，
∴$3=(2m + 4)×1$，即$2m + 4=3$，解得$m=-\frac{1}{2}$。