《2025年赢在暑假抢分计划八年级数学人教版》

9. (冷水滩区校级月考)在四边形$ABCD$中,$AD = BC$,补充一个条件使其成为平行四边形,你补充的条件是$AB=CD$(只需填一个即可).

答案： $AB=CD$

10. (泰安)如图,四边形$ABCD$为平行四边形,则点$B$的坐标为$(-2,-1)$.

答案： 解：设点$B$的坐标为$(x,y)$。
因为四边形$ABCD$是平行四边形，所以$\overrightarrow{AB}=\overrightarrow{DC}$。
已知$A(-1,2)$，$D(3,2)$，$C(2,-1)$，则$\overrightarrow{DC}=(2 - 3, -1 - 2)=(-1,-3)$，$\overrightarrow{AB}=(x - (-1),y - 2)=(x + 1,y - 2)$。
所以$\begin{cases}x + 1=-1\\y - 2=-3\end{cases}$，解得$\begin{cases}x=-2\\y=-1\end{cases}$。
点$B$的坐标为$(-2,-1)$。

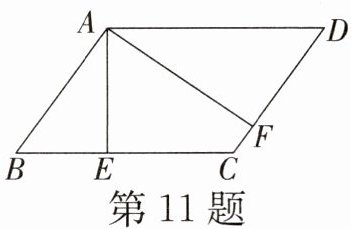
11. (黄浦区校级期末)如图,在$□ ABCD$中,$AE\perp BC$,$AF\perp CD$,垂足分别是$E$,$F$,$\angle EAF = 60^{\circ}$,$BE = 2$,$DF = 3$,则$□ ABCD$的周长为______20.

答案： 解：
∵ 四边形 $ABCD$ 是平行四边形，
∴ $AB // CD$，$AD // BC$，$\angle B = \angle D$，$\angle BAD + \angle B = 180^\circ$。
∵ $AE \perp BC$，$AF \perp CD$，
∴ $\angle AEC = \angle AFC = 90^\circ$。
在四边形 $AECF$ 中，$\angle EAF = 60^\circ$，
∴ $\angle C = 360^\circ - 90^\circ - 90^\circ - 60^\circ = 120^\circ$，
∴ $\angle B = \angle D = 180^\circ - 120^\circ = 60^\circ$。
在 $Rt\triangle ABE$ 中，$BE = 2$，$\angle B = 60^\circ$，
∴ $\angle BAE = 30^\circ$，
∴ $AB = 2BE = 4$，$AE = \sqrt{AB^2 - BE^2} = \sqrt{4^2 - 2^2} = 2\sqrt{3}$。
在 $Rt\triangle ADF$ 中，$DF = 3$，$\angle D = 60^\circ$，
∴ $\angle DAF = 30^\circ$，
∴ $AD = 2DF = 6$。
∴ 平行四边形 $ABCD$ 的周长为 $2(AB + AD) = 2(4 + 6) = 20$。
答案：20

12. (张店区校级期末)如图,在$□ ABCD$中,过对角线$BD上一点P作EF// BC$,$GH// AB$,且$CG = 3BG$,$S_{□ BEPG} = 1.5$,则$S_{□ AEPH} = $______4.5.

答案： 解：设 $ BG = x $，则 $ CG = 3x $，$ BC = BG + CG = 4x $。
因为 $ EF // BC $，$ GH // AB $，所以四边形 $ BEPG $、$ AEPH $、$ CFPG $、$ HPFD $ 均为平行四边形。
由于 $ GH // AB $，所以 $ \triangle BPG \sim \triangle DPH $，$ \triangle EBP \sim \triangle FDP $，且相似比均为 $ \frac{BG}{AD} = \frac{BG}{BC} = \frac{x}{4x} = \frac{1}{4} $。
设平行四边形 $ BEPG $ 的高为 $ h $，则其面积 $ S_{□BEPG} = BG \cdot h = x \cdot h = 1.5 $。
平行四边形 $ AEPH $ 的底为 $ AH = BG = x $（此处应为 $ AH = AD - HD $，修正：因 $ GH // AB $，$ AB = CD $，$ AG = BH $，实际 $ AEPH $ 的底为 $ AE = AB - BE $，但由相似比可知 $ \frac{BE}{AE} = \frac{BG}{CG} = \frac{1}{3} $，设 $ BE = m $，则 $ AE = 3m $）。
$ S_{□BEPG} = BE \cdot BG' = m \cdot x = 1.5 $（$ BG' $ 为平行四边形 $ BEPG $ 以 $ BE $ 为底的高），则 $ S_{□AEPH} = AE \cdot x = 3m \cdot x = 3(m \cdot x) = 3 × 1.5 = 4.5 $。
答案：4.5

13. (泰山区校级期末)在平行四边形$ABCD$中,$BF平分\angle ABC$,交$AD于点F$,$CE平分\angle BCD$,交$AD于点E$,$AB = 6$,$EF = 2$,则$BC$的长为______10或14.

答案： 解：
情况一：点E在点F右侧
∵四边形ABCD是平行四边形
∴AD//BC，AB=CD=6，AD=BC
∵BF平分∠ABC
∴∠ABF=∠FBC
∵AD//BC
∴∠AFB=∠FBC
∴∠ABF=∠AFB
∴AF=AB=6
同理，DE=CD=6
∵EF=2
∴AD=AF+DE-EF=6+6-2=10
∴BC=AD=10
情况二：点F在点E右侧
∵四边形ABCD是平行四边形
∴AD//BC，AB=CD=6，AD=BC
∵BF平分∠ABC
∴∠ABF=∠FBC
∵AD//BC
∴∠AFB=∠FBC
∴∠ABF=∠AFB
∴AF=AB=6
同理，DE=CD=6
∵EF=2
∴AD=AF+EF+DE=6+2+6=14
∴BC=AD=14
综上，BC的长为10或14。

14. (招远市期末)如图,在$\triangle ABC$中,$CE$是中线,$CD$是角平分线,$AF\perp CD交CD的延长线于点F$,$AC = 9$,$BC = 4$,则$EF$的长为______2.5.

答案： 延长AF交BC于点G。
∵CD是∠ACB的角平分线，AF⊥CD，
∴∠ACF=∠GCF，∠AFC=∠GFC=90°。
在△AFC和△GFC中，
∠ACF=∠GCF，CF=CF，∠AFC=∠GFC，
∴△AFC≌△GFC(ASA)，
∴CG=AC=9，AF=FG。
∵BC=4，
∴BG=CG-BC=9-4=5。
∵CE是△ABC的中线，
∴E为AB中点。
又
∵AF=FG，
∴EF是△ABG的中位线，
∴EF=1/2BG=1/2×5=2.5。
答案：2.5

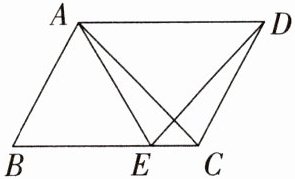
15. (7分)(2023·雁塔区校级一模)如图,在$□ ABCD$中,$E是边BC$上一点,连接$AE$,$AC$,$ED$.若$AE = AB$,求证：$AC = DE$.

答案： 证明: $ \because $ 四边形 $ABCD$ 为平行四边形,
$ \therefore AD // BC$, $AD = BC$.
$ \therefore \angle DAE = \angle AEB$.
$ \because AB = AE$,
$ \therefore \angle AEB = \angle B$.
$ \therefore \angle B = \angle DAE$.
在 $ \triangle ABC $ 和 $ \triangle EAD $ 中,
$ \begin{cases} AB = EA, \\ \angle B = \angle DAE, \\ BC = AD, \end{cases} $
$ \therefore \triangle ABC \cong \triangle EAD (SAS)$.
$ \therefore AC = DE$.

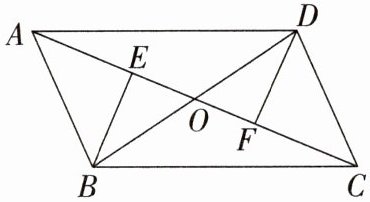
16. (7分)(鞍山)如图,在四边形$ABCD$中,$AC与BD交于点O$,$BE\perp AC$,$DF\perp AC$,垂足分别为点$E$,$F$,且$BE = DF$,$\angle ABD = \angle BDC$.求证：四边形$ABCD$是平行四边形.

答案： 证明：
∵∠ABD=∠BDC，
∴AB//CD．
∴∠BAE=∠DCF．
∵BE⊥AC，DF⊥AC，
∴∠AEB=∠CFD=90°．
在△ABE和△CDF中，
$\left\{ \begin{array}{l} ∠BAE=∠DCF, \\ ∠AEB=∠CFD, \\ BE=DF, \end{array} \right.$
∴△ABE≌△CDF（AAS）．
∴AB=CD．
∵AB//CD且AB=CD，
∴四边形ABCD是平行四边形．