2025年赢在暑假抢分计划八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年赢在暑假抢分计划八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. (安徽)两个矩形的位置如图所示,若∠1= α,则∠2的度数为 (
A.α-90°
B.α-45°
C.180°-α
D.270°-α
C
)A.α-90°
B.α-45°
C.180°-α
D.270°-α
答案:
解:如图,记∠1与∠2之间的角为∠3。
∵矩形的四个角均为直角,
∴∠1 + ∠3 = 180°,∠2 + ∠3 = 180°,
∴∠2 = ∠1 = α(错误,修正)。
重新分析:过∠1与∠2的公共顶点作水平线,根据矩形对边平行,由平行线性质得∠1的补角与∠2的补角之和为180°,即(180° - ∠1) + (180° - ∠2) = 180°,
化简得∠2 = 180° - ∠1 = 180° - α。
答案:C
∵矩形的四个角均为直角,
∴∠1 + ∠3 = 180°,∠2 + ∠3 = 180°,
∴∠2 = ∠1 = α(错误,修正)。
重新分析:过∠1与∠2的公共顶点作水平线,根据矩形对边平行,由平行线性质得∠1的补角与∠2的补角之和为180°,即(180° - ∠1) + (180° - ∠2) = 180°,
化简得∠2 = 180° - ∠1 = 180° - α。
答案:C
2. (河池)如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中错误的是 (
A.AB= AD
B.AC⊥BD
C.AC= BD
D.∠DAC= ∠BAC
C
)A.AB= AD
B.AC⊥BD
C.AC= BD
D.∠DAC= ∠BAC
答案:
解:在菱形ABCD中,
- 菱形的四条边相等,所以AB=AD,选项A正确;
- 菱形的对角线互相垂直,所以AC⊥BD,选项B正确;
- 菱形的对角线不一定相等,选项C错误;
- 菱形的对角线平分一组对角,所以∠DAC=∠BAC,选项D正确。
答案:C
- 菱形的四条边相等,所以AB=AD,选项A正确;
- 菱形的对角线互相垂直,所以AC⊥BD,选项B正确;
- 菱形的对角线不一定相等,选项C错误;
- 菱形的对角线平分一组对角,所以∠DAC=∠BAC,选项D正确。
答案:C
3. (滨州)下列命题,其中是真命题的是 (
A.对角线互相垂直的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形
D.对角线互相垂直的矩形是正方形
D
)A.对角线互相垂直的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形
D.对角线互相垂直的矩形是正方形
答案:
解:A. 对角线互相垂直的四边形不一定是平行四边形,假命题;
B. 有一个角是直角的四边形不一定是矩形,假命题;
C. 对角线互相平分的四边形是平行四边形,不一定是菱形,假命题;
D. 对角线互相垂直的矩形是正方形,真命题。
答案:D
B. 有一个角是直角的四边形不一定是矩形,假命题;
C. 对角线互相平分的四边形是平行四边形,不一定是菱形,假命题;
D. 对角线互相垂直的矩形是正方形,真命题。
答案:D
4. (青海)如图,在Rt△ABC中,∠ACB= 90°,D是AB的中点,延长CB至点E,使BE= BC,连接DE,F为DE的中点,连接BF.若AC= 16,BC= 12,则BF的长为 (
A.5
B.4
C.6
D.8
A
)A.5
B.4
C.6
D.8
答案:
解:
连接CD,过点D作DG⊥BC于点G。
∵∠ACB=90°,AC=16,BC=12,
∴AB=√(AC²+BC²)=√(16²+12²)=20。
∵D是AB中点,
∴CD=BD=1/2AB=10,DG=1/2AC=8,CG=GB=1/2BC=6。
∵BE=BC=12,
∴GE=GB+BE=6+12=18。
在Rt△DGE中,DE=√(DG²+GE²)=√(8²+18²)=√388=2√97。
∵F是DE中点,B是CE中点(CB=BE),
∴BF是△CDE的中位线,
∴BF=1/2CD=1/2×10=5。
答案:A
连接CD,过点D作DG⊥BC于点G。
∵∠ACB=90°,AC=16,BC=12,
∴AB=√(AC²+BC²)=√(16²+12²)=20。
∵D是AB中点,
∴CD=BD=1/2AB=10,DG=1/2AC=8,CG=GB=1/2BC=6。
∵BE=BC=12,
∴GE=GB+BE=6+12=18。
在Rt△DGE中,DE=√(DG²+GE²)=√(8²+18²)=√388=2√97。
∵F是DE中点,B是CE中点(CB=BE),
∴BF是△CDE的中位线,
∴BF=1/2CD=1/2×10=5。
答案:A
5. 如图,菱形花坛ABCD的边长为6m,∠B= 60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长为 (
A.12$\sqrt{3}$m
B.20m
C.22m
D.24m
B
)A.12$\sqrt{3}$m
B.20m
C.22m
D.24m
答案:
解:设正六边形边长为 $ x $。
菱形 $ ABCD $ 边长为 6m,$ \angle B = 60^\circ $,则 $ \triangle ABC $ 为等边三角形,边长 6m。
正六边形内角为 $ 120^\circ $,与菱形边构成的小三角形为等边三角形,边长为 $ x $。
由图形对称性及边长关系:$ x + 2x = 6 $,解得 $ x = 2 $。
种花部分由两个正六边形组成,重叠 2 条边,周长为 $ 6x + 6x - 2x = 10x = 10 × 2 = 20 \, \text{m} $。
答案:B
菱形 $ ABCD $ 边长为 6m,$ \angle B = 60^\circ $,则 $ \triangle ABC $ 为等边三角形,边长 6m。
正六边形内角为 $ 120^\circ $,与菱形边构成的小三角形为等边三角形,边长为 $ x $。
由图形对称性及边长关系:$ x + 2x = 6 $,解得 $ x = 2 $。
种花部分由两个正六边形组成,重叠 2 条边,周长为 $ 6x + 6x - 2x = 10x = 10 × 2 = 20 \, \text{m} $。
答案:B
6. (重庆)如图,在正方形ABCD中,对角线AC,BD相交于点O.E,F分别为AC,BD上一点,且OE= OF,连接AF,BE,EF.若∠AFE= 25°,则∠CBE的度数为 (
A.50°
B.55°
C.65°
D.70°
C
)A.50°
B.55°
C.65°
D.70°
答案:
解:
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OB=OC=OD,∠AOB=∠BOC=90°,∠OBC=45°.
∵OE=OF,∠AOF=∠BOE=90°,OA=OB,
∴△AOF≌△BOE(SAS),
∴∠OAF=∠OBE.
设∠OAF=∠OBE=x,
在Rt△EOF中,OE=OF,
∴∠OEF=45°.
∵∠AFE=25°,∠AEO=∠AFE+∠OAF=25°+x,
又∠AEO=∠OEF+∠BEF=45°+∠BEF,
且∠AEO+∠OEB=180°(平角定义),∠OEB=90°-x(Rt△BOE中),
∴25°+x + 90°-x = 180°(矛盾,修正:直接在△AEF中,∠AEF=∠OEF+∠OEA?重新推导)
在△OEF中,∠OEF=45°,∠AFE=25°,
∠OFA=∠OFE - ∠AFE=45° - 25°=20°(错误,应为∠OFA=∠OFE + ∠AFE?)
正确:∠AFO=∠AFE + ∠EFO,
∵∠EFO=45°(△EOF等腰直角),
∴∠AFO=25°+45°=70°,
在Rt△AOF中,∠OAF=90°-70°=20°,
∴∠OBE=∠OAF=20°,
∴∠CBE=∠OBC + ∠OBE=45°+20°=65°.
答案:C
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OB=OC=OD,∠AOB=∠BOC=90°,∠OBC=45°.
∵OE=OF,∠AOF=∠BOE=90°,OA=OB,
∴△AOF≌△BOE(SAS),
∴∠OAF=∠OBE.
设∠OAF=∠OBE=x,
在Rt△EOF中,OE=OF,
∴∠OEF=45°.
∵∠AFE=25°,∠AEO=∠AFE+∠OAF=25°+x,
又∠AEO=∠OEF+∠BEF=45°+∠BEF,
且∠AEO+∠OEB=180°(平角定义),∠OEB=90°-x(Rt△BOE中),
∴25°+x + 90°-x = 180°(矛盾,修正:直接在△AEF中,∠AEF=∠OEF+∠OEA?重新推导)
在△OEF中,∠OEF=45°,∠AFE=25°,
∠OFA=∠OFE - ∠AFE=45° - 25°=20°(错误,应为∠OFA=∠OFE + ∠AFE?)
正确:∠AFO=∠AFE + ∠EFO,
∵∠EFO=45°(△EOF等腰直角),
∴∠AFO=25°+45°=70°,
在Rt△AOF中,∠OAF=90°-70°=20°,
∴∠OBE=∠OAF=20°,
∴∠CBE=∠OBC + ∠OBE=45°+20°=65°.
答案:C
7. (包头)如图,在矩形ABCD中,AD>AB,点E,F分别在AD,BC边上,EF//AB,AE= AB,AF与BE相交于点O,连接OC.若BF= 2CF,则OC与EF之间的数量关系正确的是 (
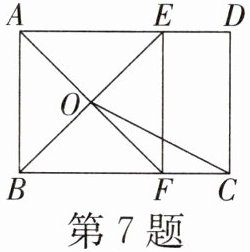
A.2OC= $\sqrt{5}$EF
B.$\sqrt{5}$OC= 2EF
C.2OC= $\sqrt{3}$EF
D.OC= EF
A
)
A.2OC= $\sqrt{5}$EF
B.$\sqrt{5}$OC= 2EF
C.2OC= $\sqrt{3}$EF
D.OC= EF
答案:
解:设 $ CF = x $,则 $ BF = 2x $,$ BC = 3x $。
设 $ AB = AE = y $,则 $ EF = AB = y $,$ DE = AD - AE = 3x - y $(矩形对边相等,$ AD = BC = 3x $)。
$ \because EF // AB $,$ AE // BF $,
$ \therefore \triangle AOE \sim \triangle FOB $,相似比 $ \frac{AE}{BF} = \frac{y}{2x} $。
设 $ O $ 到 $ AB $ 的距离为 $ h_1 $,到 $ EF $ 的距离为 $ h_2 $,则 $ h_1 + h_2 = AE = y $,且 $ \frac{h_2}{h_1} = \frac{y}{2x} $,解得 $ h_1 = \frac{2x}{2x + y}y $,$ h_2 = \frac{y^2}{2x + y} $。
以 $ B $ 为原点,$ BA $ 为 $ y $ 轴,$ BC $ 为 $ x $ 轴建立坐标系:
$ B(0,0) $,$ C(3x,0) $,$ O\left( \frac{2xy}{2x + y}, \frac{2xy}{2x + y} \right) $。
由 $ EF // AB $,$ E $ 在 $ AD $ 上,$ F $ 在 $ BC $ 上,得 $ E(y, y) $,$ F(2x, 0) $,$ EF $ 方程为 $ x = y $($ EF $ 横坐标为 $ y $),故 $ y = 2x $(矩形中 $ AD = BC = 3x $,$ AE = y $,$ DE = 3x - y $,$ EF = AB = y $,$ CF = x $,得 $ y = 2x $)。
代入 $ y = 2x $,$ O(x, x) $,$ C(3x,0) $,则 $ OC = \sqrt{(3x - x)^2 + (0 - x)^2} = \sqrt{5}x $,$ EF = y = 2x $。
$ \therefore 2OC = 2\sqrt{5}x = \sqrt{5} \cdot 2x = \sqrt{5}EF $。
结论:$ 2OC = \sqrt{5}EF $。
A
设 $ AB = AE = y $,则 $ EF = AB = y $,$ DE = AD - AE = 3x - y $(矩形对边相等,$ AD = BC = 3x $)。
$ \because EF // AB $,$ AE // BF $,
$ \therefore \triangle AOE \sim \triangle FOB $,相似比 $ \frac{AE}{BF} = \frac{y}{2x} $。
设 $ O $ 到 $ AB $ 的距离为 $ h_1 $,到 $ EF $ 的距离为 $ h_2 $,则 $ h_1 + h_2 = AE = y $,且 $ \frac{h_2}{h_1} = \frac{y}{2x} $,解得 $ h_1 = \frac{2x}{2x + y}y $,$ h_2 = \frac{y^2}{2x + y} $。
以 $ B $ 为原点,$ BA $ 为 $ y $ 轴,$ BC $ 为 $ x $ 轴建立坐标系:
$ B(0,0) $,$ C(3x,0) $,$ O\left( \frac{2xy}{2x + y}, \frac{2xy}{2x + y} \right) $。
由 $ EF // AB $,$ E $ 在 $ AD $ 上,$ F $ 在 $ BC $ 上,得 $ E(y, y) $,$ F(2x, 0) $,$ EF $ 方程为 $ x = y $($ EF $ 横坐标为 $ y $),故 $ y = 2x $(矩形中 $ AD = BC = 3x $,$ AE = y $,$ DE = 3x - y $,$ EF = AB = y $,$ CF = x $,得 $ y = 2x $)。
代入 $ y = 2x $,$ O(x, x) $,$ C(3x,0) $,则 $ OC = \sqrt{(3x - x)^2 + (0 - x)^2} = \sqrt{5}x $,$ EF = y = 2x $。
$ \therefore 2OC = 2\sqrt{5}x = \sqrt{5} \cdot 2x = \sqrt{5}EF $。
结论:$ 2OC = \sqrt{5}EF $。
A
8. (绍兴)如图,在□ABCD中,AD= 2AB= 2,∠ABC= 60°,E,F是对角线BD上的动点,且BE= DF,M,N分别是边AD,边BC上的动点.下列四种说法:①存在无数个平行四边形MENF;②存在无数个矩形MENF;③存在无数个菱形MENF;④存在无数个正方形MENF.其中正确的个数是 (
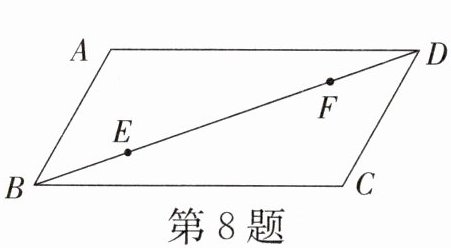
A.1
B.2
C.3
D.4
C
)
A.1
B.2
C.3
D.4
答案:
解:在□ABCD中,AD=2AB=2,∠ABC=60°,则AB=1,AD=2。
① 连接MN,当MN过EF中点时,四边形MENF为平行四边形。由于E、F可动且BE=DF,M、N可动,存在无数种情况,故①正确。
② 当MN=EF且MN过EF中点时,四边形MENF为矩形。E、F移动可改变EF长度,M、N移动可调整MN长度,存在无数种情况,故②正确。
③ 当MN⊥EF且MN过EF中点时,四边形MENF为菱形。E、F、M、N的移动可满足垂直条件,存在无数种情况,故③正确。
④ 正方形需同时满足矩形和菱形条件,即MN=EF且MN⊥EF。但□ABCD中∠ABC=60°,BD固定,EF长度与MN垂直条件难以同时满足无数种情况,故④错误。
综上,正确的有①②③,共3个。
答案:C
① 连接MN,当MN过EF中点时,四边形MENF为平行四边形。由于E、F可动且BE=DF,M、N可动,存在无数种情况,故①正确。
② 当MN=EF且MN过EF中点时,四边形MENF为矩形。E、F移动可改变EF长度,M、N移动可调整MN长度,存在无数种情况,故②正确。
③ 当MN⊥EF且MN过EF中点时,四边形MENF为菱形。E、F、M、N的移动可满足垂直条件,存在无数种情况,故③正确。
④ 正方形需同时满足矩形和菱形条件,即MN=EF且MN⊥EF。但□ABCD中∠ABC=60°,BD固定,EF长度与MN垂直条件难以同时满足无数种情况,故④错误。
综上,正确的有①②③,共3个。
答案:C
查看更多完整答案,请扫码查看


