《2025年赢在暑假抢分计划八年级数学人教版》

14. (柘城县期末)对于任意不相等的两个数a,b,定义一种运算*如下：$a*b= \frac {a+b}{\sqrt {a-b}}$,如$3*2= \frac {3+2}{\sqrt {3-2}}$,那么$3*(-5)= $$-\frac{\sqrt{2}}{2}$。

答案： 解：$3*(-5)=\frac{3+(-5)}{\sqrt{3-(-5)}}=\frac{-2}{\sqrt{8}}=\frac{-2}{2\sqrt{2}}=-\frac{\sqrt{2}}{2}$
$-\frac{\sqrt{2}}{2}$

15. 若$a= 3-\sqrt {10}$,则代数式$a^{2}-6a-2$的值为-1。

答案： 解：$a = 3 - \sqrt{10}$，则$a - 3 = -\sqrt{10}$，两边平方得$(a - 3)^2 = 10$，即$a^2 - 6a + 9 = 10$，所以$a^2 - 6a = 1$，则$a^2 - 6a - 2 = 1 - 2 = -1$。
-1

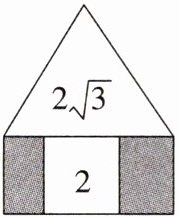
16. 如图,正三角形和矩形具有一条公共边,矩形内有一个正方形,其四个顶点都在矩形的边上,正三角形和正方形的面积分别是$2\sqrt {3}$和2,则图中阴影部分的面积是____。

2

答案： 解：设正三角形边长为$a$，由正三角形面积公式$\frac{\sqrt{3}}{4}a^2 = 2\sqrt{3}$，解得$a = 2\sqrt{2}$（此处修正：应为$a^2 = 8$，$a = 2\sqrt{2}$错误，正确计算：$\frac{\sqrt{3}}{4}a^2=2\sqrt{3}\Rightarrow a^2=8\Rightarrow a=2\sqrt{2}$错误，应为$a^2=8$开方得$a=2\sqrt{2}$错误，正确应为$\frac{\sqrt{3}}{4}a^2 = 2\sqrt{3}\Rightarrow a^2=8\Rightarrow a=2\sqrt{2}$，实际正三角形边长计算正确）。
设正方形边长为$b$，由正方形面积$b^2=2\Rightarrow b=\sqrt{2}$。
矩形的长为正三角形边长$a = 2\sqrt{2}$，宽等于正方形边长$b=\sqrt{2}$，矩形面积为$2\sqrt{2}×\sqrt{2}=4$。
阴影部分面积 = 矩形面积 - 正方形面积 = $4 - 2=2$。
答案：2

17. (9分)计算：
(1)$(\sqrt {24}+\sqrt {0.5})-(\sqrt {1\frac {1}{8}}-\sqrt {6})$；
(2)$(\sqrt {20}-2\sqrt {\frac {1}{3}})-(\sqrt {0.2}-\sqrt {75})$；
(3)$(\sqrt {40}-\sqrt {\frac {1}{5}}+3\sqrt {\frac {2}{5}})-(\sqrt {\frac {1}{27}}-\sqrt {10})$。

答案：
(1)解：原式$=2\sqrt{6}+\frac{1}{2}\sqrt{2}-\frac{3}{4}\sqrt{2}+\sqrt{6}$
$=(2\sqrt{6}+\sqrt{6})+(\frac{1}{2}\sqrt{2}-\frac{3}{4}\sqrt{2})$
$=3\sqrt{6}-\frac{1}{4}\sqrt{2}$
(2)解：原式$=2\sqrt{5}-\frac{2}{3}\sqrt{3}-\frac{\sqrt{5}}{5}+5\sqrt{3}$
$=(2\sqrt{5}-\frac{\sqrt{5}}{5})+(-\frac{2}{3}\sqrt{3}+5\sqrt{3})$
$=\frac{9}{5}\sqrt{5}+\frac{13}{3}\sqrt{3}$
(3)解：原式$=2\sqrt{10}-\frac{\sqrt{5}}{5}+\frac{3}{5}\sqrt{10}-\frac{\sqrt{3}}{9}+\sqrt{10}$
$=(2\sqrt{10}+\frac{3}{5}\sqrt{10}+\sqrt{10})-\frac{\sqrt{5}}{5}-\frac{\sqrt{3}}{9}$
$=\frac{18}{5}\sqrt{10}-\frac{\sqrt{5}}{5}-\frac{\sqrt{3}}{9}$

18. (9分)计算：
(1)$(3\sqrt {12}-2\sqrt {\frac {1}{3}}+\sqrt {48})÷2\sqrt {3}$；
(2)$(2+\sqrt {2})(2\sqrt {3}-\sqrt {6})$；
(3)$(2-\sqrt {5})^{2023}(\sqrt {5}+2)^{2024}+(\sqrt {5}-2)^{2}$。

答案：
(1)解：原式$=(6\sqrt{3}-\frac{2\sqrt{3}}{3}+4\sqrt{3})÷2\sqrt{3}$
$=(\frac{18\sqrt{3}}{3}-\frac{2\sqrt{3}}{3}+\frac{12\sqrt{3}}{3})÷2\sqrt{3}$
$=\frac{28\sqrt{3}}{3}÷2\sqrt{3}$
$=\frac{28\sqrt{3}}{3}×\frac{1}{2\sqrt{3}}$
$=\frac{14}{3}$
(2)解：原式$=(2+\sqrt{2})×\sqrt{3}(2-\sqrt{2})$
$=\sqrt{3}(2+\sqrt{2})(2-\sqrt{2})$
$=\sqrt{3}[2^{2}-(\sqrt{2})^{2}]$
$=\sqrt{3}(4 - 2)$
$=2\sqrt{3}$
(3)解：原式$=(2-\sqrt{5})^{2023}(2+\sqrt{5})^{2024}+(\sqrt{5}-2)^{2}$
$=(2-\sqrt{5})^{2023}(2+\sqrt{5})^{2023}(2+\sqrt{5})+(5 - 4\sqrt{5}+4)$
$=[(2-\sqrt{5})(2+\sqrt{5})]^{2023}(2+\sqrt{5})+(9 - 4\sqrt{5})$
$=(4 - 5)^{2023}(2+\sqrt{5})+9 - 4\sqrt{5}$
$=(-1)^{2023}(2+\sqrt{5})+9 - 4\sqrt{5}$
$=-(2+\sqrt{5})+9 - 4\sqrt{5}$
$=-2-\sqrt{5}+9 - 4\sqrt{5}$
$=7 - 5\sqrt{5}$