《2025年赢在暑假抢分计划八年级数学人教版》

1. 在$Rt△ABC$中,$∠A$,$∠B$,$∠C$所对的边分别为a,b,c,$∠A$是直角,则下列结论错误的是 (A)
A.$c^{2}-a^{2}= b^{2}$
B.$a^{2}= b^{2}+c^{2}$
C.$c^{2}= a^{2}-b^{2}$
D.$b^{2}= a^{2}-c^{2}$

答案： 解：在$Rt△ABC$中，$∠A$是直角，根据勾股定理可得$a^{2}=b^{2}+c^{2}$。
由此变形可得：$b^{2}=a^{2}-c^{2}$，$c^{2}=a^{2}-b^{2}$。
所以选项B、C、D正确，选项A错误。
答案：A

2. 如果一直角三角形的两边长分别为3和5,则第三边长是 (C)
A.4
B.$\sqrt{34}$
C.4或$\sqrt{34}$
D.以上都不正确

答案： 解：
情况一：当3和5为直角边时，第三边长为$\sqrt{3^2 + 5^2} = \sqrt{34}$；
情况二：当5为斜边，3为直角边时，第三边长为$\sqrt{5^2 - 3^2} = 4$。
综上，第三边长是4或$\sqrt{34}$。
答案：C

3. 在$Rt△ABC$中,$∠ACB = 90^{\circ}$,$AB = 3$,则$AB^{2}+BC^{2}+AC^{2}$的值是 (B)
A.9
B.18
C.20
D.24

答案： 解：在$Rt△ABC$中，$∠ACB = 90^{\circ}$，根据勾股定理得$AC^{2} + BC^{2} = AB^{2}$。
因为$AB = 3$，所以$AB^{2} = 3^{2} = 9$，即$AC^{2} + BC^{2} = 9$。
则$AB^{2} + BC^{2} + AC^{2} = AB^{2} + (AC^{2} + BC^{2}) = 9 + 9 = 18$。
答案：B

4. (蚌山区校级期中)如图,将一根长为16 cm的橡皮筋固定在笔直的木棒上,两端点分别记为点A,点B,然后将中点C向上拉升6 cm,则橡皮筋被拉长了 (A)
A.4 cm
B.5 cm
C.6 cm
D.7 cm

答案： 解：
∵橡皮筋原长16cm，C为AB中点，
∴AC=BC=8cm。
设拉升后中点为D，CD=6cm，且CD⊥AB。
在Rt△ACD中，AC=8cm，CD=6cm，
由勾股定理得：AD=$\sqrt{AC^2 + CD^2}=\sqrt{8^2 + 6^2}=10$cm。
同理BD=10cm。
拉伸后橡皮筋长度为AD+BD=20cm。
拉长的长度为20-16=4cm。
答案：A

5. (大观区校级期中)如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A,B,D的面积依次为6,10,24,则正方形C的面积为 (C)
A.4
B.6
C.8
D.12

答案： C

6. (广陵区校级期末)已知$△ABC$中,$AB = 17$,$AC = 10$,BC边上的高$AD = 8$,则边BC的长为 (C)
A.21
B.9
C.21或9
D.17或10

答案： 解：在$Rt\triangle ABD$中，$AB=17$，$AD=8$，由勾股定理得：$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{17^{2}-8^{2}}=15$。
在$Rt\triangle ACD$中，$AC=10$，$AD=8$，由勾股定理得：$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{10^{2}-8^{2}}=6$。
当高$AD$在$\triangle ABC$内部时，$BC=BD+CD=15+6=21$；
当高$AD$在$\triangle ABC$外部时，$BC=BD-CD=15-6=9$。
综上，$BC$的长为21或9。
答案：C

7. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为 (C)

A.0.7米
B.1.5米
C.2.2米
D.2.4米

答案： 解：设梯子长度为$ l $米，梯子底端到右墙角的距离为$ x $米。
当梯子斜靠在左墙时，由勾股定理得：$ l^2 = 0.7^2 + 2.4^2 $
$ 0.7^2 + 2.4^2 = 0.49 + 5.76 = 6.25 $，所以$ l^2 = 6.25 $，$ l = 2.5 $（米）。
当梯子斜靠在右墙时，顶端距离地面2米，由勾股定理得：$ x^2 + 2^2 = l^2 $
即$ x^2 + 4 = 6.25 $，$ x^2 = 2.25 $，$ x = 1.5 $（米）。
小巷宽度为梯子底端到左墙角距离与到右墙角距离之和：$ 0.7 + 1.5 = 2.2 $（米）。
答案：C

8. 如图,圆柱形玻璃杯,高为12 cm,底面周长为18 cm。在杯内离杯底4 cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4 cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 (A)
A.15 cm
B.$\sqrt{97}$ cm
C.12 cm
D.18 cm

答案： 解：将圆柱侧面展开，得到一个长方形。
长方形的长为底面周长18cm，宽为圆柱的高12cm。
点A在杯外壁离上沿4cm处，其对称点A'在展开图中离下沿4cm处，离长方形一边距离为9cm（18÷2）。
点C在杯内离杯底4cm处，在展开图中离下沿4cm处，离长方形另一边距离为9cm。
A'与C在展开图中横向距离为9cm，纵向距离为12cm（12 - 4 + 4）。
最短距离为A'C的长度：$\sqrt{9^2 + 12^2} = 15$cm。
答案：A

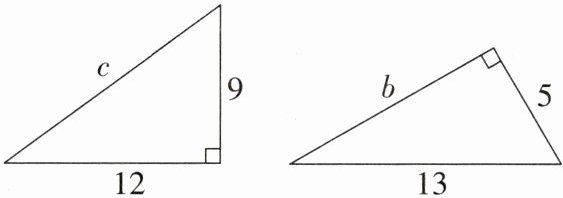
9. 求图中直角三角形中未知边的长度：c = 15,b = 12。

答案： 解：左图：
由勾股定理得 $ c^2 = 12^2 + 9^2 = 144 + 81 = 225 $，
$ c = \sqrt{225} = 15 $。
右图：
由勾股定理得 $ b^2 = 13^2 - 5^2 = 169 - 25 = 144 $，
$ b = \sqrt{144} = 12 $。
15 12