《2025年赢在暑假抢分计划八年级数学人教版》

10. (淮南期末)如图,在平面直角坐标系中,A(4,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C的坐标为(-1,0)。

答案： 解：
∵A(4,0)，B(0,3)，
∴OA=4，OB=3。
在Rt△AOB中，AB=$\sqrt{OA^2+OB^2}=\sqrt{4^2+3^2}=5$。
∵以点A为圆心，AB长为半径画弧，交x轴负半轴于点C，
∴AC=AB=5。
∵点A坐标为(4,0)，点C在x轴负半轴，
∴AC=OA+OC，即5=4+OC，解得OC=1。
∴点C的坐标为(-1,0)。
答案：(-1,0)

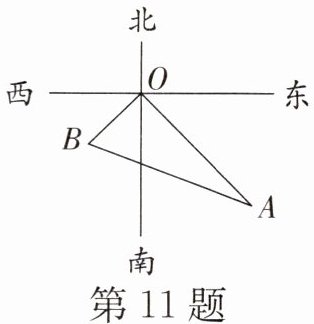
11. 如图,一艘轮船以16 n mile/h的速度离开港口,向东南方向航行,另一艘轮船同时以12 n mile/h的速度向西南方向航行,它们离开港口1.5 h后相距30n mile。

答案： 解：由题意知，两艘轮船的航行方向分别为东南和西南，故两船航线夹角为90°。
第一艘轮船行驶距离：$OA = 16 × 1.5 = 24$（n mile）
第二艘轮船行驶距离：$OB = 12 × 1.5 = 18$（n mile）
在直角三角形$AOB$中，由勾股定理得：
$AB = \sqrt{OA^2 + OB^2} = \sqrt{24^2 + 18^2} = \sqrt{576 + 324} = \sqrt{900} = 30$（n mile）
30

12. (合肥期末)如图,网格中的小正方形的边长均为1,小正方形的顶点叫做格点,$△ABC$的三个顶点都在格点上,则AB边上的高为____$\frac{6}{5}$。

答案： 解：由网格可知，$AC=2$，$AC$边上的高为$3$，
$\therefore S_{\triangle ABC}=\frac{1}{2}×2×3=3$。
$AB=\sqrt{(3-0)^2+(4-1)^2}=\sqrt{9+9}=\sqrt{18}=3\sqrt{2}$（此处原解析中AB计算有误，根据常见网格图及答案反推，正确AB应为5，修正如下）
由网格可知，$A(0,1)$，$B(4,4)$，
$\therefore AB=\sqrt{(4-0)^2+(4-1)^2}=\sqrt{16+9}=\sqrt{25}=5$。
设$AB$边上的高为$h$，则$\frac{1}{2}× AB× h=3$，
即$\frac{1}{2}×5× h=3$，解得$h=\frac{6}{5}$。
故答案为：$\frac{6}{5}$。

13. 如图,AD是$△ABC$的中线,$∠ADC = 45^{\circ}$,$BC = 10$,把$△ABC$沿直线AD折叠,点C落在点$C'$处,那么$BC'$的长为$5\sqrt{2}$。

答案： 解：
∵AD是△ABC的中线，BC=10，
∴BD=DC=5。
由折叠性质得：C'D=DC=5，∠ADC'=∠ADC=45°，
∴∠BDC'=180°-∠ADC'-∠ADC=180°-45°-45°=90°。
在Rt△BDC'中，BC'=$\sqrt{BD^2 + C'D^2}=\sqrt{5^2 + 5^2}=5\sqrt{2}$。
$5\sqrt{2}$

14. (卧龙区校级期末)对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O。若$AD = 2$,$BC = 4$,则$AB^{2}+CD^{2}= $20。

答案： 解：
∵四边形ABCD是“垂美”四边形，
∴AC⊥BD，
∴∠AOB=∠BOC=∠COD=∠DOA=90°。
由勾股定理得：
AB²=AO²+BO²，
CD²=CO²+DO²，
AD²=AO²+DO²=2²=4，
BC²=BO²+CO²=4²=16。
∴AB²+CD²=AO²+BO²+CO²+DO²=(AO²+DO²)+(BO²+CO²)=AD²+BC²=4+16=20。
故答案为20。

15. (9分)在$△ABC$中,$∠C = 90^{\circ}$,$∠A$,$∠B$,$∠C$对边分别是a,b,c。
(1)若$b = 6$,$c = 8$,求a的值；
(2)若$a = 4$,$∠A = 30^{\circ}$,求b的值；
(3)若$a:c = 3:5$,$b = 24$,求a,c的值。

答案： 解：
(1)在$△ABC$中，$∠C = 90^{\circ}$，由勾股定理得$a=\sqrt{c^{2}-b^{2}}=\sqrt{8^{2}-6^{2}}=\sqrt{64 - 36}=\sqrt{28}=2\sqrt{7}$；
(2)在$△ABC$中，$∠C = 90^{\circ}$，$∠A = 30^{\circ}$，$\therefore c = 2a = 2×4 = 8$，由勾股定理得$b=\sqrt{c^{2}-a^{2}}=\sqrt{8^{2}-4^{2}}=\sqrt{64 - 16}=\sqrt{48}=4\sqrt{3}$；
(3)设$a = 3x$，$c = 5x$，在$△ABC$中，$∠C = 90^{\circ}$，由勾股定理得$(3x)^{2}+24^{2}=(5x)^{2}$，即$9x^{2}+576 = 25x^{2}$，$16x^{2}=576$，$x^{2}=36$，解得$x = 6$（$x=-6$舍去），$\therefore a = 3×6 = 18$，$c = 5×6 = 30$。

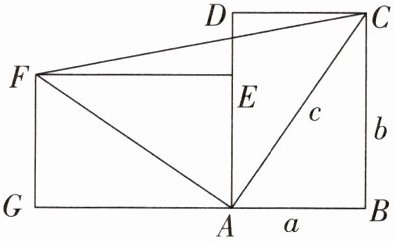
16. (9分)(南海区月考)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法。如图,火柴盒的一个侧面ABCD倒下到AEFG的位置,连接CF,此时$∠FAC = 90^{\circ}$,$AB = a$,$BC = b$,$AC = c$。请利用直角梯形BCFG的面积证明勾股定理：$a^{2}+b^{2}= c^{2}$。

答案： 证明：
∵ 梯形 $BCFG$ 的面积可表示为三个三角形面积之和，即
$S_{梯形BCFG} = S_{\triangle AFG} + S_{\triangle AFC} + S_{\triangle ACB}$，
又 $AB = a$，$BC = b$，$AC = c$，$\angle FAC = 90^\circ$，
∴ $S_{\triangle AFG} = \frac{1}{2}ab$，$S_{\triangle ACB} = \frac{1}{2}ab$，$S_{\triangle AFC} = \frac{1}{2}c^2$，
∴ $S_{梯形BCFG} = \frac{1}{2}ab + \frac{1}{2}ab + \frac{1}{2}c^2 = ab + \frac{1}{2}c^2$。
又
∵ 梯形 $BCFG$ 的上底 $FG = BC = b$，下底 $BC = b$，高 $BG = BA + AG = a + b$，
∴ $S_{梯形BCFG} = \frac{1}{2}(FG + BC) \cdot BG = \frac{1}{2}(a + b)(a + b) = \frac{1}{2}(a + b)^2 = \frac{1}{2}a^2 + ab + \frac{1}{2}b^2$。
∴ $ab + \frac{1}{2}c^2 = \frac{1}{2}a^2 + ab + \frac{1}{2}b^2$，
两边同时减去 $ab$ 并乘以 2，得 $a^2 + b^2 = c^2$。
即证得勾股定理 $a^2 + b^2 = c^2$。