《2025年赢在暑假抢分计划八年级数学人教版》

8. 如图是本地区一种产品$30$天的销售图象,图$1是产品日销售量y$(单位:件)与时间$t$(单位:天)的函数关系,图$2是一件产品的销售利润z$(单位:元)与时间$t$(单位:天)的函数关系.已知日销售利润$=日销售量×$一件产品的销售利润.下列结论错误的是( C )

A.第$24天的销售量为200$件
B.第$10天销售一件产品的利润是15$元
C.第$12天与第30$天这两天的日销售利润相等
D.第$30天的日销售利润是750$元

答案： 解：A. 由图1知，第24天的销售量为200件，正确。
B. 图2中，设0≤t≤20时，z=kt+b，将(0,25)，(20,5)代入得：25=b，5=20k+b，解得k=-1，b=25，
∴z=-t+25。当t=10时，z=-10+25=15，正确。
C. 图1中，设0≤t≤24时，y=mt+n，将(0,100)，(24,200)代入得：100=n，200=24m+n，解得m=25/6，n=100，
∴y=25/6 t+100。当t=12时，y=25/6×12+100=150，z=-12+25=13，利润=150×13=1950；第30天，y=150（图1），z=5（图2），利润=150×5=750，1950≠750，错误。
D. 第30天，y=150，z=5，利润=150×5=750，正确。
结论错误的是C。
答案：C

9. (大庆)写出一个过点$D(0,1)且y随x$增大而减小的一次函数解析式$y = -x + 1$（答案不唯一）.

答案： 设该一次函数解析式为$y = kx + b$（$k\neq0$）。
因为函数过点$D(0,1)$，所以将$x = 0$，$y = 1$代入解析式可得$1 = k×0 + b$，即$b = 1$。
又因为$y$随$x$增大而减小，所以$k ＜ 0$。令$k = -1$，则该一次函数解析式为$y = -x + 1$。
$y = -x + 1$（答案不唯一）

10. 若一次函数$y = -x + a与一次函数y = x$$+ b的图象的交点坐标为(m,8)$,则$a + b = $16.

答案： 解：因为一次函数$y = -x + a$与$y = x + b$的图象交点坐标为$(m,8)$，
所以将$(m,8)$代入$y = -x + a$，得$8 = -m + a$，即$a = m + 8$；
将$(m,8)$代入$y = x + b$，得$8 = m + b$，即$b = 8 - m$。
则$a + b = (m + 8) + (8 - m) = 16$。
16

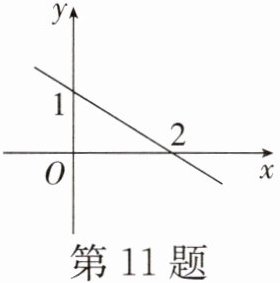
11. (鼓楼区校级期末)已知一次函数$y = kx + b$的图象如图所示,则关于$x的不等式kx + b$$＞ 1$的解集是$x ＜ 0$.

答案： 解：由图象可知，一次函数$y = kx + b$的图象过点$(0,1)$，且$y$随$x$的增大而减小。
当$x = 0$时，$y = 1$。
因为$y$随$x$的增大而减小，所以当$x ＜ 0$时，$y ＞ 1$。
即不等式$kx + b ＞ 1$的解集是$x ＜ 0$。
$x ＜ 0$

12. (辽宁)如图,直线$y = 2x + 4与x轴交于点A$,与$y轴交于点B$,点$D为OB$的中点,$□ OCDE的顶点C在x$轴上,顶点$E在直线AB$上,则$□ OCDE$的面积为____2.

答案： 解：
对于直线$y = 2x + 4$，
- 令$y = 0$，得$2x + 4 = 0$，解得$x = -2$，则$A(-2, 0)$；
- 令$x = 0$，得$y = 4$，则$B(0, 4)$。
点$D$为$OB$中点，$OB = 4$，故$OD = \frac{1}{2}OB = 2$，则$D(0, 2)$。
在$□OCDE$中，$DE // OC$，$OC$在$x$轴上，故$DE$垂直于$y$轴，点$E$与$D$纵坐标相同，均为$2$。
点$E$在直线$AB$上，将$y = 2$代入$y = 2x + 4$，得$2 = 2x + 4$，解得$x = -1$，则$E(-1, 2)$。
$DE$长度为点$E$与$D$横坐标差的绝对值：$DE = |0 - (-1)| = 1$。
$□OCDE$的面积为$DE × OD = 1 × 2 = 2$。
答案：$2$

13. (德阳)如图,已知点$A(-2,3)$,$B(2,1)$,直线$y = kx + k经过点P(-1,0)$.试探究:直线与线段$AB有交点时k$的变化情况,猜想$k$的取值范围是$k \leq -3$或$k \geq \frac{1}{3}$.

答案： 解：
直线$y=kx+k$恒过点$P(-1,0)$。
当直线过点$A(-2,3)$时，代入得$3=-2k+k$，解得$k=-3$；
当直线过点$B(2,1)$时，代入得$1=2k+k$，解得$k=\frac{1}{3}$。
观察图像，直线与线段$AB$有交点时，$k \leq -3$或$k \geq \frac{1}{3}$。
$k \leq -3$或$k \geq \frac{1}{3}$

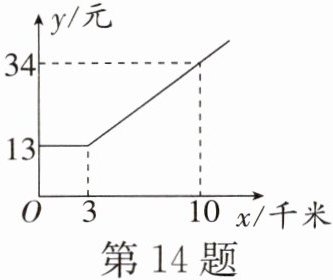
14. (青浦区模拟)图中反映某网约车平台收费$y$(元)与所行驶的路程$x$(千米)的函数关系,根据图中的信息,当小明通过该网约车从家到机场共收费$64$元,若车速始终保持$60\ \text{km/h}$,不考虑其它因素(红绿灯、堵车等),他从家到机场需要$\frac{1}{3}$小时.

答案： 由图可知，当$x \leq 3$时，$y = 13$元。当$x ＞ 3$时，设$y = kx + b$，将$(3,13)$，$(10,34)$代入得：
$\begin{cases}3k + b = 13 \\10k + b = 34\end{cases}$
解得$k = 3$，$b = 4$，即$y = 3x + 4$（$x ＞ 3$）。
当$y = 64$时，$64 = 3x + 4$，解得$x = 20$千米。
时间$t = \frac{20}{60} = \frac{1}{3}$小时。
$\frac{1}{3}$

15. (10分)(1)请在平面直角坐标系中画出函数$y = 2x - 4$的图象;
(2)判断点$A(-3,-2)$,$B(3,2)是否在函数y = 2x - 4$的图象上?

答案：
(1) 当$x=0$时，$y=2×0 - 4=-4$，得到点$(0,-4)$；当$y=0$时，$0=2x - 4$，解得$x=2$，得到点$(2,0)$。在平面直角坐标系中描出点$(0,-4)$和$(2,0)$，过这两点作直线，即为函数$y = 2x - 4$的图象。
(2) 对于点$A(-3,-2)$，当$x=-3$时，$y=2×(-3)-4=-6 - 4=-10\neq -2$，所以点$A$不在函数图象上；对于点$B(3,2)$，当$x=3$时，$y=2×3 - 4=6 - 4=2$，所以点$B$在函数图象上。
综上，点$A$不在函数图象上，点$B$在函数图象上。