《2025年练习生高中数学选择性必修第一册人教A版》

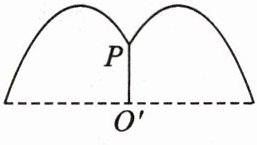
9. 如图，花坛水池中央有一喷泉，水管O'P = 1 m，水从喷头P喷出后呈抛物线状，先向上至最高点然后落下. 若最高点距水面2 m，P距抛物线的对称轴1 m，问：水池的直径至少应设计多长(精确到整数位)?

答案： 【解】如图，以抛物线的顶点为原点，过顶点与焦点的直线为$y$轴，建立平面直角坐标系，则$P(-1,-1)$.设抛物线的方程为$x^{2}=-2py(p\gt0)$.将点$P$的坐标代入抛物线方程，得$p=\frac{1}{2}$，所以抛物线的方程为$x^{2}=-y$.又$B(x_{B},-2)$，所以$x_{B}^{2}=2$，所以$x_{B}=\sqrt{2}$（负值已舍去），所以$|O'B|=\sqrt{2}+1$.所以，根据对称性知，水池直径为$2(\sqrt{2}+1)m$，约为$5m$.

10. 如图是一种加热水和食物的太阳灶，上面装有可旋转的抛物面形的反光镜，镜的轴截面是抛物线的一部分，盛水和食物的容器放在抛物线的焦点处，容器由若干根等长的铁筋焊接在一起的架子支撑. 已知镜口圆的直径为12 m，镜深2 m.
（1）建立适当的平面直角坐标系，求抛物线的焦点位置；
（2）若把盛水和食物的容器近似地看作点，试求容器的每根铁筋的长度.

答案： 【解】 - （1）如图，在反光镜的轴截面内建立平面直角坐标系，使反光镜的顶点（即抛物线的顶点）与原点重合，$x$轴垂直于镜口直径. 由题意，得$A(2,6)$.设抛物线的方程为$y^{2}=2px(p\gt0)$，则$36 = 2p\times2$，解得$p = 9$，所以抛物线的标准方程是$y^{2}=18x$，所以焦点$F(4.5,0)$，所以焦点在经过抛物面顶点且与镜口圆面垂直的直线上，距顶点$4.5m$处. - （2）因为盛水的容器在焦点处，所以$A,F$两点间的距离即为每根铁筋长，所以每根铁筋长为$2+\frac{p}{2}=2 + 4.5 = 6.5(m)$. 

11. (多选)下列方程的图形为抛物线的是（ ）
A. |x + 1| - $\sqrt{x^{2}+y^{2}}$ = 0
B. |y - 2| = $\sqrt{(x + 1)^{2}+(y - 2)^{2}}$
C. $\sqrt{(x - 2)^{2}+(y - 3)^{2}}$ = $\frac{|3x + 4y - 11|}{\sqrt{3^{2}+4^{2}}}$
D. x² - 2x - y + 3 = 0

答案： ACD

12. [2022·云南曲靖罗平一中高二期末]已知抛物线x² = my(m＞0)上的点(x₀,1)到该抛物线的焦点F的距离为2，则m = （ ）
A. 1
B. 2
C. 4
D. 6

答案： C

13. [2022·北京二中高二月考]已知P(x₀,2)为抛物线C:y² = 2px(p＞0)上一点，点P到抛物线C的焦点的距离与它到y轴的距离之比为3 : 2，则p = （ ）
A. $\sqrt{2}$
B. 2
C. 2$\sqrt{2}$
D. 3

答案： A

14. 已知点A为抛物线y² = 4x上的动点，以点A为圆心的圆M与y轴相切，抛物线的焦点为F，线段AF与圆M相交于点P，则|PF| = （ ）
A. 4
B. 2
C. 1
D. $\frac{1}{2}$

答案： C

15. 若动点M(x,y)满足5$\sqrt{(x - 1)^{2}+(y - 2)^{2}}$ = |3x - 4y + 12|，则点M的轨迹是（ ）
A. 圆
B. 椭圆
C. 双曲线
D. 抛物线

答案： D

16. 一抛物线状的拱桥，当桥顶离水面1 m时，水面宽4 m，若水面下降3 m，则水面宽为（ ）
A. 6 m
B. 7 m
C. 8 m
D. 9 m

答案： C