2025年练习生高中数学选择性必修第一册人教A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第一册人教A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
9. [2022·广东揭阳普宁勤建学校高二阶段练习]若$\{a,b,c\}$构成空间的一个基底,则下列向量共面的是( )
A. $2a - b,a + b - c,7a + 5b + 3c$
B. $2a + b,a + b + c,7a + 5b + 3c$
C. $2a + b,a + b + c,6a + 2b + 4c$
D. $2a - b,a + b - c,6a + 4b + 2c$
A. $2a - b,a + b - c,7a + 5b + 3c$
B. $2a + b,a + b + c,7a + 5b + 3c$
C. $2a + b,a + b + c,6a + 2b + 4c$
D. $2a - b,a + b - c,6a + 4b + 2c$
答案:
B
10.(多选)[2021·浙江杭州第二中学高二期中]已知$\{a,b,c\}$是空间的一个基底,则下列说法正确的是( )
A. 存在不全为零的实数x,y,z,使得$xa + yb + zc = 0$
B. 对空间任一向量p,存在唯一的有序实数组$(x,y,z)$,使得$p = xa + yb + zc$
C. 在a,b,c中,能与$a + b,a - b$构成空间另一个基底的只有c
D. 不存在另一个基底$\{a',b',c'\}$,使得$a + 2b + 3c = a' + 2b' + 3c'$
A. 存在不全为零的实数x,y,z,使得$xa + yb + zc = 0$
B. 对空间任一向量p,存在唯一的有序实数组$(x,y,z)$,使得$p = xa + yb + zc$
C. 在a,b,c中,能与$a + b,a - b$构成空间另一个基底的只有c
D. 不存在另一个基底$\{a',b',c'\}$,使得$a + 2b + 3c = a' + 2b' + 3c'$
答案:
BC
11.(多选)如图,在平行六面体ABCD - A₁B₁C₁D₁中,$AB = AD = AA_{1}=1$,$\angle BAD=\frac{\pi}{3}$,$\angle BAA_{1}=\angle DAA_{1}=\frac{\pi}{4}$,则下列说法正确的是( )
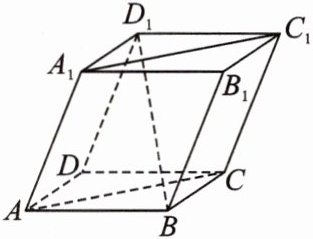
A. $\{\overrightarrow{AA_{1}},\overrightarrow{BD_{1}},\overrightarrow{AB}\}$不能构成空间的一个基底
B. $|\overrightarrow{BD_{1}}|=\sqrt{2}$
C. $BD\perp$平面$ACC_{1}A_{1}$
D. 直线$BD_{1}$与直线$AA_{1}$所成的角为$\frac{\pi}{4}$

A. $\{\overrightarrow{AA_{1}},\overrightarrow{BD_{1}},\overrightarrow{AB}\}$不能构成空间的一个基底
B. $|\overrightarrow{BD_{1}}|=\sqrt{2}$
C. $BD\perp$平面$ACC_{1}A_{1}$
D. 直线$BD_{1}$与直线$AA_{1}$所成的角为$\frac{\pi}{4}$
答案:
BCD
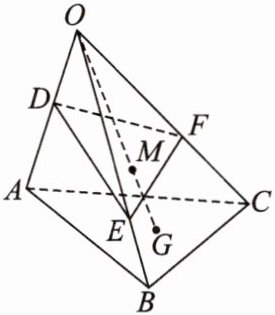
12. 如图,在三棱锥O - ABC中,点G为底面△ABC的重心,点M是线段OG上靠近点G的三等分点,过点M的平面分别交棱OA,OB,OC于点D,E,F,若$\overrightarrow{OD}=k\overrightarrow{OA},\overrightarrow{OE}=m\overrightarrow{OB},\overrightarrow{OF}=n\overrightarrow{OC}$,则$\frac{1}{k}+\frac{1}{m}+\frac{1}{n}=$_______.

答案:
$\frac {9}{2}$
13. [2023·广东广州真光中学高二阶段练习]如图,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F,G分别是AB,AD,CD的中点.设$\overrightarrow{AB}=a,\overrightarrow{AC}=b,\overrightarrow{AD}=c$.
(1)求证:$EG\perp AB$.
(2)求异面直线AG和CE所成角的余弦值.
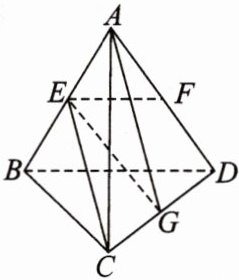
(1)求证:$EG\perp AB$.
(2)求异面直线AG和CE所成角的余弦值.

答案:
(1)【证明】**连接$DE$,如图. 因为空间四边形$ABCD$的每条边和对角线长都等于$1$,所以$AC = BC$,$BD = AD$. 又$E$是$AB$的中点,所以$CE\perp AB$,$DE\perp AB$. 因为$CE\cap DE = E$,$CE,DE\subset$平面$CDE$,所以$AB\perp$平面$CDE$. 因为$EG\subset$平面$CDE$,所以$AB\perp EG$. **
(2)【解】**由题意得$\triangle ABC,\triangle ACD,\triangle ABD$均为等边三角形且边长为$1$,所以$AG = EC=\frac{\sqrt{3}}{2}$. 易得$\overrightarrow{AG}=\frac{1}{2}(b + c)$,$\overrightarrow{EC}=\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{AC})=\frac{1}{2}(\overrightarrow{AC}-\overrightarrow{AB}+\overrightarrow{AC})=b-\frac{1}{2}a$. 所以$\overrightarrow{AG}\cdot\overrightarrow{EC}=\frac{1}{2}(b + c)\cdot(b-\frac{1}{2}a)=\frac{1}{2}b^{2}-\frac{1}{4}a\cdot b+\frac{1}{2}c\cdot b-\frac{1}{4}a\cdot c=\frac{1}{2}-\frac{1}{4}|a||b|\cos60^{\circ}+\frac{1}{2}|c|\cdot|b|\cos60^{\circ}-\frac{1}{4}|a||c|\cos60^{\circ}=\frac{1}{2}-\frac{1}{8}+\frac{1}{4}-\frac{1}{8}=\frac{1}{2}$. 设异面直线$AG$和$CE$所成的角为$\theta$,则$\cos\theta=|\cos\langle\overrightarrow{AG},\overrightarrow{EC}\rangle|=\frac{|\overrightarrow{AG}\cdot\overrightarrow{EC}|}{|\overrightarrow{AG}||\overrightarrow{EC}|}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}\times\frac{\sqrt{3}}{2}}=\frac{2}{3}$.
(1)【证明】**连接$DE$,如图. 因为空间四边形$ABCD$的每条边和对角线长都等于$1$,所以$AC = BC$,$BD = AD$. 又$E$是$AB$的中点,所以$CE\perp AB$,$DE\perp AB$. 因为$CE\cap DE = E$,$CE,DE\subset$平面$CDE$,所以$AB\perp$平面$CDE$. 因为$EG\subset$平面$CDE$,所以$AB\perp EG$. **
(2)【解】**由题意得$\triangle ABC,\triangle ACD,\triangle ABD$均为等边三角形且边长为$1$,所以$AG = EC=\frac{\sqrt{3}}{2}$. 易得$\overrightarrow{AG}=\frac{1}{2}(b + c)$,$\overrightarrow{EC}=\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{AC})=\frac{1}{2}(\overrightarrow{AC}-\overrightarrow{AB}+\overrightarrow{AC})=b-\frac{1}{2}a$. 所以$\overrightarrow{AG}\cdot\overrightarrow{EC}=\frac{1}{2}(b + c)\cdot(b-\frac{1}{2}a)=\frac{1}{2}b^{2}-\frac{1}{4}a\cdot b+\frac{1}{2}c\cdot b-\frac{1}{4}a\cdot c=\frac{1}{2}-\frac{1}{4}|a||b|\cos60^{\circ}+\frac{1}{2}|c|\cdot|b|\cos60^{\circ}-\frac{1}{4}|a||c|\cos60^{\circ}=\frac{1}{2}-\frac{1}{8}+\frac{1}{4}-\frac{1}{8}=\frac{1}{2}$. 设异面直线$AG$和$CE$所成的角为$\theta$,则$\cos\theta=|\cos\langle\overrightarrow{AG},\overrightarrow{EC}\rangle|=\frac{|\overrightarrow{AG}\cdot\overrightarrow{EC}|}{|\overrightarrow{AG}||\overrightarrow{EC}|}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}\times\frac{\sqrt{3}}{2}}=\frac{2}{3}$.
14. 如图,已知正方体ABCD - A₁B₁C₁D₁的棱长为1,P,Q,R分别在AB,CC₁,D₁A₁上,并满足$\frac{AP}{PB}=\frac{CQ}{QC_{1}}=\frac{D_{1}R}{RA_{1}}=\frac{a}{1 - a}(0 < a < 1)$.设$\overrightarrow{AB}=i,\overrightarrow{AD}=j,\overrightarrow{AA_{1}}=k$.
(1)用i,j,k表示$\overrightarrow{PQ},\overrightarrow{PR}$;
(2)设△PQR的重心为G,用i,j,k表示$\overrightarrow{DG}$;
(3)当$RG\perp DG$时,求a的取值范围.
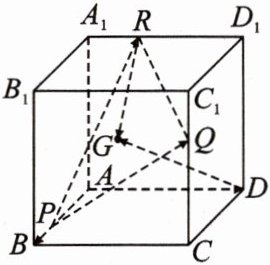
(1)用i,j,k表示$\overrightarrow{PQ},\overrightarrow{PR}$;
(2)设△PQR的重心为G,用i,j,k表示$\overrightarrow{DG}$;
(3)当$RG\perp DG$时,求a的取值范围.

答案:
【解】**
(1)$\overrightarrow{PQ}=\overrightarrow{PB}+\overrightarrow{BC}+\overrightarrow{CQ}=(1 - a)\overrightarrow{AB}+\overrightarrow{AD}+a\overrightarrow{CC_{1}}=(1 - a)\cdot i + j+ak$,$\overrightarrow{PR}=\overrightarrow{PA}+\overrightarrow{AA_{1}}+\overrightarrow{A_{1}R}=-a\overrightarrow{AB}+\overrightarrow{AA_{1}}+(1 - a)\overrightarrow{A_{1}D_{1}}=-ai + k+(1 - a)j$.
(2)$\overrightarrow{DG}=\overrightarrow{DC}+\overrightarrow{CQ}+\overrightarrow{QG}=\overrightarrow{AB}+a\overrightarrow{CC_{1}}+\frac{2}{3}(\overrightarrow{QP}+\frac{1}{2}\overrightarrow{PR})=i + ak+\frac{2}{3}[(a - 1)i - j - ak]+\frac{1}{3}[-ai + k+(1 - a)j]=\frac{1}{3}(a + 1)i+\frac{1}{3}(a + 1)k-\frac{1}{3}(a + 1)j$.
(3)$\because\overrightarrow{RG}\perp\overrightarrow{DG}$,$\therefore\overrightarrow{RG}\cdot\overrightarrow{DG}=0$. 又$\overrightarrow{RG}=\overrightarrow{RD}+\overrightarrow{DG}=\overrightarrow{RD_{1}}+\overrightarrow{D_{1}D}+\overrightarrow{DG}=a\overrightarrow{A_{1}D_{1}}-\overrightarrow{DD_{1}}+\overrightarrow{DG}=aj - k+\frac{1}{3}(a + 1)i+\frac{1}{3}(a + 1)k-\frac{1}{3}(a + 1)j=\frac{1}{3}(a + 1)i+\frac{1}{3}(a - 2)\cdot k+\frac{1}{3}(2a - 1)j$,$\therefore\overrightarrow{RG}\cdot\overrightarrow{DG}=[\frac{1}{3}(a + 1)i+\frac{1}{3}(a - 2)k+\frac{1}{3}(2a - 1)j]\cdot[\frac{1}{3}(a + 1)i+\frac{1}{3}(a + 1)k-\frac{1}{3}(a + 1)j]=\frac{1}{9}(a + 1)^{2}+\frac{1}{9}(a - 2)(a + 1)-\frac{1}{9}(2a - 1)(a + 1)=\frac{1}{9}(a^{2}+2a + 1+a^{2}-a - 2-2a^{2}-a + 1)=0$. 即对任意$0\lt a\lt1$,都有$\overrightarrow{RG}\perp\overrightarrow{DG}$,故$a$的取值范围为$(0,1)$.
(1)$\overrightarrow{PQ}=\overrightarrow{PB}+\overrightarrow{BC}+\overrightarrow{CQ}=(1 - a)\overrightarrow{AB}+\overrightarrow{AD}+a\overrightarrow{CC_{1}}=(1 - a)\cdot i + j+ak$,$\overrightarrow{PR}=\overrightarrow{PA}+\overrightarrow{AA_{1}}+\overrightarrow{A_{1}R}=-a\overrightarrow{AB}+\overrightarrow{AA_{1}}+(1 - a)\overrightarrow{A_{1}D_{1}}=-ai + k+(1 - a)j$.
(2)$\overrightarrow{DG}=\overrightarrow{DC}+\overrightarrow{CQ}+\overrightarrow{QG}=\overrightarrow{AB}+a\overrightarrow{CC_{1}}+\frac{2}{3}(\overrightarrow{QP}+\frac{1}{2}\overrightarrow{PR})=i + ak+\frac{2}{3}[(a - 1)i - j - ak]+\frac{1}{3}[-ai + k+(1 - a)j]=\frac{1}{3}(a + 1)i+\frac{1}{3}(a + 1)k-\frac{1}{3}(a + 1)j$.
(3)$\because\overrightarrow{RG}\perp\overrightarrow{DG}$,$\therefore\overrightarrow{RG}\cdot\overrightarrow{DG}=0$. 又$\overrightarrow{RG}=\overrightarrow{RD}+\overrightarrow{DG}=\overrightarrow{RD_{1}}+\overrightarrow{D_{1}D}+\overrightarrow{DG}=a\overrightarrow{A_{1}D_{1}}-\overrightarrow{DD_{1}}+\overrightarrow{DG}=aj - k+\frac{1}{3}(a + 1)i+\frac{1}{3}(a + 1)k-\frac{1}{3}(a + 1)j=\frac{1}{3}(a + 1)i+\frac{1}{3}(a - 2)\cdot k+\frac{1}{3}(2a - 1)j$,$\therefore\overrightarrow{RG}\cdot\overrightarrow{DG}=[\frac{1}{3}(a + 1)i+\frac{1}{3}(a - 2)k+\frac{1}{3}(2a - 1)j]\cdot[\frac{1}{3}(a + 1)i+\frac{1}{3}(a + 1)k-\frac{1}{3}(a + 1)j]=\frac{1}{9}(a + 1)^{2}+\frac{1}{9}(a - 2)(a + 1)-\frac{1}{9}(2a - 1)(a + 1)=\frac{1}{9}(a^{2}+2a + 1+a^{2}-a - 2-2a^{2}-a + 1)=0$. 即对任意$0\lt a\lt1$,都有$\overrightarrow{RG}\perp\overrightarrow{DG}$,故$a$的取值范围为$(0,1)$.
查看更多完整答案,请扫码查看


