《2025年练习生高中数学选择性必修第一册人教A版》

18. 某地居民的居住区域大致呈如图所示的五边形,近似由一个正方形和两个等腰直角三角形组成. 若$AB = 60$ km,$AE = CD = 30$ km,现准备建一个电视转播台,理想方案是转播台距五边形各顶点距离的平方和最小,图中$P_1,P_2,P_3,P_4$是$AC$的五等分点,则转播台应建在 ( )

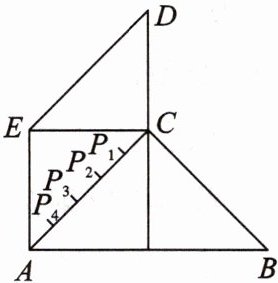
A. $P_1$处
B. $P_2$处
C. $P_3$处
D. $P_4$处

答案： 本题可分直线$l$的斜率存在和不存在两种情况进行讨论，再根据点到直线的距离公式判断是否存在满足条件的直线。\n**当直线$l$的斜率不存在时：**
此时直线$l$的方程为$x = 2$，根据点$(x_0,y_0)$到直线$x = a$的距离公式$d = \vert x_0 - a\vert$，可得原点$(0,0)$到直线$x = 2$的距离为$\vert 0 - 2\vert = 2\neq 6$，所以直线$l$的斜率不存在时不满足条件。\n**当直线$l$的斜率存在时：**
设直线$l$的方程为$y + 1 = k(x - 2)$，即$kx - y - 2k - 1 = 0$。
根据点$(x_0,y_0)$到直线$Ax + By + C = 0$（$A$、$B$不同时为$0$）的距离公式$d = \frac{\vert Ax_0 + By_0 + C\vert}{\sqrt{A^2 + B^2}}$，可得原点$(0,0)$到直线$kx - y - 2k - 1 = 0$的距离为$\frac{\vert - 2k - 1\vert}{\sqrt{k^2 + 1}} = 6$。
两边同时平方可得$\frac{(2k + 1)^2}{k^2 + 1} = 36$，即$(2k + 1)^2 = 36(k^2 + 1)$，展开可得：
$\begin{aligned}4k^2 + 4k + 1&= 36k^2 + 36\\32k^2 - 4k + 35&= 0\end{aligned}$
对于一元二次方程$ax^2 + bx + c = 0$（$a\neq 0$），其判别式$\Delta = b^2 - 4ac$，在方程$32k^2 - 4k + 35 = 0$中，$a = 32$，$b = -4$，$c = 35$，则$\Delta = (-4)^2 - 4\times32\times35 = 16 - 4480 = -4464\lt 0$，所以此方程无实数解，即不存在满足条件的斜率$k$。
综上，不存在满足条件的直线$l$。

19. 设$m\in\mathbf{R}$,已知直线$l_1:(m + 1)x + my + 2 - m = 0$,过点$(1,2)$作直线$l_2$,且$l_1// l_2$,则直线$l_1$与$l_2$之间距离的最大值是________.

答案： 本题可先设出线段中点$M$的坐标，再根据点$M$到两平行直线的距离相等求出点$M$的坐标，最后根据两点式求出直线$l$的方程。\n**步骤一：设点$M$的坐标**
因为点$M$在直线$x + y - 3 = 0$上，所以可设$M(t,3 - t)$。\n**步骤二：根据点$M$到两平行直线的距离相等求出$t$的值**
因为点$M$是直线$l$被平行直线$l_1$与$l_2$所截线段的中点，所以点$M$到$l_1$与$l_2$的距离相等。
根据点$(x_0,y_0)$到直线$Ax + By + C = 0$（$A$、$B$不同时为$0$）的距离公式$d = \frac{\vert Ax_0 + By_0 + C\vert}{\sqrt{A^2 + B^2}}$，可得点$M(t,3 - t)$到直线$l_1$：$x - y + 1 = 0$的距离为$\frac{\vert t - (3 - t) + 1\vert}{\sqrt{1^2 + (-1)^2}} = \frac{\vert 2t - 2\vert}{\sqrt{2}}$，点$M(t,3 - t)$到直线$l_2$：$x - y - 1 = 0$的距离为$\frac{\vert t - (3 - t) - 1\vert}{\sqrt{1^2 + (-1)^2}} = \frac{\vert 2t - 4\vert}{\sqrt{2}}$。
则$\frac{\vert 2t - 2\vert}{\sqrt{2}} = \frac{\vert 2t - 4\vert}{\sqrt{2}}$，即$\vert 2t - 2\vert = \vert 2t - 4\vert$，两边同时平方可得：
$(2t - 2)^2 = (2t - 4)^2$
展开可得：
$4t^2 - 8t + 4 = 4t^2 - 16t + 16$
移项可得：
$8t = 12$
解得$t = \frac{3}{2}$。
所以$M(\frac{3}{2},\frac{3}{2})$。\n**步骤三：求直线$l$的方程**
已知直线$l$过点$A(2,4)$和点$M(\frac{3}{2},\frac{3}{2})$，根据直线的两点式方程$\frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}$（其中$(x_1,y_1)$，$(x_2,y_2)$为直线上两点），可得直线$l$的方程为：
$\frac{y - 4}{\frac{3}{2} - 4} = \frac{x - 2}{\frac{3}{2} - 2}$
$\frac{y - 4}{-\frac{5}{2}} = \frac{x - 2}{-\frac{1}{2}}$
即$5x - y - 6 = 0$。
综上，直线$l$的方程为$5x - y - 6 = 0$。

20. 在平面直角坐标系内,已知$A(1,2)$,$B(1,5)$,$C(3,6)$,$D(7,-1)$,则平面内任意一点到点$A$与点$C$的距离之和的最小值为________,平面内到$A,B,C,D$的距离之和最小的点的坐标是________.

答案： 本题可先求出直线$l$的方程，进而得到$P$、$Q$两点的坐标，再求出$PR$、$QS$的长度以及$PQ$的长度，最后根据梯形面积公式求出四边形$PQSR$的面积并求其最小值。\n**步骤一：求直线$l$的方程以及$P$、$Q$两点的坐标**
已知直线$l$过点$A(1,1)$且斜率为$-m(m\gt 0)$，根据直线的点斜式方程$y - y_0 = k(x - x_0)$（其中$(x_0,y_0)$为直线上一点，$k$为直线斜率），可得直线$l$的方程为$y - 1 = -m(x - 1)$，即$y = -mx + m + 1$。
令$y = 0$，可得$0 = -mx + m + 1$，解得$x = \frac{m + 1}{m}$，所以$P(\frac{m + 1}{m},0)$；
令$x = 0$，可得$y = m + 1$，所以$Q(0,m + 1)$。\n**步骤二：求$PR$、$QS$的长度**
根据点$(x_0,y_0)$到直线$Ax + By + C = 0$（$A$、$B$不同时为$0$）的距离公式$d = \frac{\vert Ax_0 + By_0 + C\vert}{\sqrt{A^2 + B^2}}$，可得点$P(\frac{m + 1}{m},0)$到直线$2x + y = 0$的距离$PR$为：
$PR = \frac{\vert 2\times\frac{m + 1}{m} + 0\vert}{\sqrt{2^2 + 1^2}} = \frac{\vert \frac{2m + 2}{m}\vert}{\sqrt{5}} = \frac{2m + 2}{\sqrt{5}m}$
点$Q(0,m + 1)$到直线$2x + y = 0$的距离$QS$为：
$QS = \frac{\vert 2\times 0 + (m + 1)\vert}{\sqrt{2^2 + 1^2}} = \frac{\vert m + 1\vert}{\sqrt{5}} = \frac{m + 1}{\sqrt{5}}$\n**步骤三：求$PQ$的长度**
根据两点间距离公式$\vert PQ\vert = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$，可得：
$\vert PQ\vert = \sqrt{(\frac{m + 1}{m} - 0)^2 + (0 - (m + 1))^2} = \sqrt{(\frac{m + 1}{m})^2 + (m + 1)^2} = (m + 1)\sqrt{\frac{1}{m^2} + 1}$\n**步骤四：求四边形$PQSR$的面积$S$**
因为$PR\perp 2x + y = 0$，$QS\perp 2x + y = 0$，所以$PR// QS$，则四边形$PQSR$为梯形，根据梯形面积公式$S = \frac{1}{2}(a + b)h$（其中$a$、$b$为梯形的上底和下底，$h$为梯形的高），可得：
$\begin{aligned}S&=\frac{1}{2}(PR + QS)\cdot \vert PQ\vert\\&=\frac{1}{2}(\frac{2m + 2}{\sqrt{5}m} + \frac{m + 1}{\sqrt{5}})\cdot (m + 1)\sqrt{\frac{1}{m^2} + 1}\\&=\frac{1}{2}\cdot\frac{(2m + 2) + m(m + 1)}{\sqrt{5}m}\cdot (m + 1)\sqrt{\frac{1 + m^2}{m^2}}\\&=\frac{1}{2}\cdot\frac{(m + 1)(m + 2)}{\sqrt{5}m}\cdot (m + 1)\frac{\sqrt{m^2 + 1}}{m}\\&=\frac{(m + 1)^2(m + 2)\sqrt{m^2 + 1}}{2\sqrt{5}m^2}\end{aligned}$\n**步骤五：求四边形$PQSR$面积的最小值**
令$t = m + \frac{1}{m}(m\gt 0)$，根据均值不等式$m + \frac{1}{m} \geqslant 2\sqrt{m\times\frac{1}{m}} = 2$（当且仅当$m = \frac{1}{m}$，即$m = 1$时取等号），则$t\geqslant 2$。
将$S$进行变形可得：
$\begin{aligned}S&=\frac{(m^2 + 2m + 1)(m + 2)\sqrt{m^2 + 1}}{2\sqrt{5}m^2}\\&=\frac{(m^2 + 1 + 2m)(m + \frac{1}{m} + 2 - \frac{1}{m})\sqrt{m^2 + 1}}{2\sqrt{5}m^2}\\&=\frac{(t^2 + 2)(t + 2 - \frac{1}{m})\sqrt{t^2 - 2}}{2\sqrt{5}}\end{aligned}$
当$m = 1$时，$t = 2$，此时$S$取得最小值为：
$\begin{aligned}S_{min}&=\frac{(1 + 1)^2(1 + 2)\sqrt{1^2 + 1}}{2\sqrt{5}\times 1^2}\\&=\frac{4\times 3\times\sqrt{2}}{2\sqrt{5}}\\&=\frac{6\sqrt{10}}{5}\end{aligned}$
综上，四边形$PQSR$的面积的最小值为$\frac{6\sqrt{10}}{5}$。

21. 著名数学家华罗庚曾说过“数无形时少直觉,形少数时难入微”. 事实上,很多代数问题都可以转化为几何问题加以解决,如:$\sqrt{(x - a)^2+(y - b)^2}$可以转化为平面上点$M(x,y)$与点$N(a,b)$的距离. 结合上述观点,可得$\sqrt{x^2 - 4x + 20}+\sqrt{x^2 - 2x + 10}$的最小值为________.

答案： $5\sqrt {2}$

22. 是否存在直线$l$,使得直线$l$过点$P(2,-1)$,且原点到直线$l$的距离为6? 若存在,求出直线$l$的方程;若不存在,请说明理由.

答案： 【解】方法一：不存在. 理由如下：若直线$l$过点$P$，则当原点$O$到直线$l$的距离最大时，直线$l$与$OP$垂直，此时最大距离为$OP=\sqrt{2^2+(-1)^2}=\sqrt{5}$. 而$6\gt\sqrt{5}$，故不存在这样的直线$l$. 方法二：若直线$l$的斜率不存在，则直线$l$的方程为$x = 2$，此时原点到直线$l$的距离为$2$，不符合题意. 若直线$l$的斜率存在，则设直线$l$的方程为$y + 1 = k(x - 2)$，即$kx - y - 2k - 1 = 0$，此时原点到直线$l$的距离为$\frac{|2k + 1|}{\sqrt{k^2+1}}$. 令$\frac{|2k + 1|}{\sqrt{k^2+1}}=6$，整理得$32k^2-4k + 35 = 0$，则$\Delta=16-4\times32\times35\lt0$，方程无实根，所以没有符合题意的直线$l$. 综上所述，不存在符合题意的直线$l$. 

23. 已知直线$l$过点$A(2,4)$,且被平行直线$l_1:x - y + 1 = 0$与$l_2:x - y - 1 = 0$所截的线段中点$M$在直线$x + y - 3 = 0$上,求直线$l$的方程.

答案： 存在；若求出结果，还需检验其充分性. 23. 【解】方法一：$\because$点$M$在直线$x + y - 3 = 0$上，$\therefore$设点$M$的坐标为$(t,3 - t)$，则点$M$到$l_1$，$l_2$的距离相等，即$\frac{|t-(3 - t)+1|}{\sqrt{2}}=\frac{|t-(3 - t)-1|}{\sqrt{2}}$，解得$t=\frac{3}{2}$.$\therefore M(\frac{3}{2},\frac{3}{2})$. 又直线$l$过点$A(2,4)$，由两点式得$\frac{y-\frac{3}{2}}{4-\frac{3}{2}}=\frac{x-\frac{3}{2}}{2-\frac{3}{2}}$，即$5x - y - 6 = 0$. 故直线$l$的方程为$5x - y - 6 = 0$. 方法二：设与$l_1$，$l_2$平行且距离相等的直线$l_3:x - y + C = 0$，由两平行直线间的距离公式得$\frac{|C - 1|}{\sqrt{2}}=\frac{|C + 1|}{\sqrt{2}}$，解得$C = 0$. 则$l_3:x - y = 0$. 又点$M$在$l_3$上，且点$M$在直线$x + y - 3 = 0$上，联立成方程组$\begin{cases}x - y = 0\\x + y - 3 = 0\end{cases}$，解得$\begin{cases}x=\frac{3}{2}\\y=\frac{3}{2}\end{cases}$.$\therefore M(\frac{3}{2},\frac{3}{2})$. 又直线$l$过点$A(2,4)$，故由两点式得直线$l$的方程为$5x - y - 6 = 0$.

24. 已知过点$A(1,1)$且斜率为$-m(m ＞ 0)$的直线$l$与$x$轴、$y$轴分别交于$P,Q$两点,分别过点$P,Q$作直线$2x + y = 0$的垂线,垂足分别为$R,S$,求四边形$PQSR$的面积的最小值.

答案： 【解】由题意，得直线$l$的方程为$y - 1=-m(x - 1)$，即$y=-mx + 1 + m$. 令$x = 0$，得$y = 1 + m$；令$y = 0$，得$x = 1+\frac{1}{m}$. 所以$P(1+\frac{1}{m},0)$，$Q(0,1 + m)$. 从而直线$PR$和$QS$的方程分别为$x - 2y-\frac{m + 1}{m}=0$和$x - 2y+2(m + 1)=0$. 又$PR\parallel QS$，所以$|RS|=\frac{|2m + 2+1+\frac{1}{m}|}{\sqrt{5}}=\frac{2m+\frac{1}{m}+3}{\sqrt{5}}$. 由点到直线的距离公式，得$|PR|=\frac{2+\frac{2}{m}}{\sqrt{5}}$，$|QS|=\frac{m + 1}{\sqrt{5}}$. 所以$S_{四边形PQSR}=\frac{1}{2}(\frac{2+\frac{2}{m}}{\sqrt{5}}+\frac{m + 1}{\sqrt{5}})\cdot\frac{2m+\frac{1}{m}+3}{\sqrt{5}}=\frac{1}{5}(m+\frac{1}{m}+\frac{9}{4})^2-\frac{1}{80}\geqslant\frac{1}{5}(2+\frac{9}{4})^2-\frac{1}{80}\geqslant\frac{18}{5}$，当且仅当$m=\frac{1}{m}$，即$m = 1$时等号成立，所以四边形$PQSR$的面积的最小值为$\frac{18}{5}$.