2025年练习生高中数学选择性必修第一册人教A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第一册人教A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
12. (多选)若直线$ax + by + c = 0$同时经过第一、二、四象限,则$a,b,c$应满足( )
A. $ab>0$
B. $bc<0$
C. $ab<0$
D. $bc>0$
A. $ab>0$
B. $bc<0$
C. $ab<0$
D. $bc>0$
答案:
AB
13. 已知直线$a_{1}x + b_{1}y + 1 = 0$和直线$a_{2}x + b_{2}y + 1 = 0$都过点$A(2,1)$,则过点$P_{1}(a_{1},b_{1})$和点$P_{2}(a_{2},b_{2})$的直线方程是( )
A. $2x + y + 1 = 0$
B. $2x - y + 1 = 0$
C. $2x + y - 1 = 0$
D. $x + 2y + 1 = 0$
A. $2x + y + 1 = 0$
B. $2x - y + 1 = 0$
C. $2x + y - 1 = 0$
D. $x + 2y + 1 = 0$
答案:
A
14. 已知直线$l:5ax - 5y - a + 3 = 0$.
(1)求证:不论$a$为何值,直线$l$总经过第一象限.
(2)为使直线$l$不经过第二象限,求$a$的取值范围.
(1)求证:不论$a$为何值,直线$l$总经过第一象限.
(2)为使直线$l$不经过第二象限,求$a$的取值范围.
答案:
(1)证明:将直线$l$的方程变形为$y-\frac{3}{5}=a(x - \frac{1}{5})$,所以直线$l$恒过定点$(\frac{1}{5},\frac{3}{5})$,而点$(\frac{1}{5},\frac{3}{5})$在第一象限,所以不论$a$为何值,直线$l$总经过第一象限.
(2)直线$l$的方程可化为$y = ax+\frac{3 - a}{5}$,因为直线$l$不经过第二象限,则$\begin{cases}a\geqslant0\\\frac{3 - a}{5}\leqslant0\end{cases}$,解得$a\geqslant3$,所以$a$的取值范围是$[3,+\infty)$.
(1)证明:将直线$l$的方程变形为$y-\frac{3}{5}=a(x - \frac{1}{5})$,所以直线$l$恒过定点$(\frac{1}{5},\frac{3}{5})$,而点$(\frac{1}{5},\frac{3}{5})$在第一象限,所以不论$a$为何值,直线$l$总经过第一象限.
(2)直线$l$的方程可化为$y = ax+\frac{3 - a}{5}$,因为直线$l$不经过第二象限,则$\begin{cases}a\geqslant0\\\frac{3 - a}{5}\leqslant0\end{cases}$,解得$a\geqslant3$,所以$a$的取值范围是$[3,+\infty)$.
15. 已知直线$l_{1},l_{2}$均过点$P(1,2)$.
(1)若直线$l_{1}$过点$A(-1,3)$,且$l_{1}\perp l_{2}$,求直线$l_{2}$的方程;
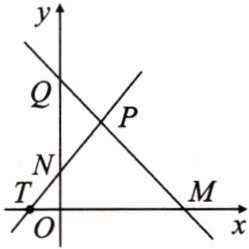
(2)如图,$O$为原点,若直线$l_{1}$的斜率为$k$,其中$0<k\leqslant2$,且与$y$轴交于点$N$,与$x$轴交于点$T$,直线$l_{2}$过点$Q(0,\frac{2}{k^{2}} + 2)$,且与$x$轴交于点$M$,求直线$l_{1},l_{2}$与两坐标轴围成的四边形$PNOM$面积的最小值.
(1)若直线$l_{1}$过点$A(-1,3)$,且$l_{1}\perp l_{2}$,求直线$l_{2}$的方程;
(2)如图,$O$为原点,若直线$l_{1}$的斜率为$k$,其中$0<k\leqslant2$,且与$y$轴交于点$N$,与$x$轴交于点$T$,直线$l_{2}$过点$Q(0,\frac{2}{k^{2}} + 2)$,且与$x$轴交于点$M$,求直线$l_{1},l_{2}$与两坐标轴围成的四边形$PNOM$面积的最小值.

答案:
(1)直线$l_{1}$的斜率$k_{1}=\frac{3 - 2}{-1 - 1}=-\frac{1}{2}$,因为$l_{1}\perp l_{2}$,所以直线$l_{2}$的斜率$k_{2}=2$,又直线$l_{2}$过点$P(1,2)$,所以直线$l_{2}$的方程为$y - 2 = 2(x - 1)$,即$2x - y = 0$.
(2)直线$l_{1}$的方程为$y - 2 = k(x - 1)$,令$x = 0$,得$y = 2 - k$,所以$N(0,2 - k)$;令$y = 0$,得$x = 1-\frac{2}{k}$,所以$T(1-\frac{2}{k},0)$.
直线$l_{2}$的斜率$k_{l_{2}}=\frac{2-( \frac{2}{k^{2}} + 2)}{1-0}=-\frac{2}{k^{2}}$,则直线$l_{2}$的方程为$y - 2 = -\frac{2}{k^{2}}(x - 1)$,令$y = 0$,得$x = k^{2}+1$,所以$M(k^{2}+1,0)$.
所以四边形$PNOM$的面积$S = S_{\triangle OPM}-S_{\triangle ONT}=\frac{1}{2}(k^{2}+1)\times2-\frac{1}{2}(1 - \frac{2}{k})(2 - k)=k^{2}+\frac{2}{k}$.
令$f(k)=k^{2}+\frac{2}{k}(0<k\leqslant2)$,则$f^\prime(k)=2k-\frac{2}{k^{2}}=\frac{2(k^{3}-1)}{k^{2}}$,令$f^\prime(k)=0$,得$k = 1$.
当$0<k<1$时,$f^\prime(k)<0$,$f(k)$单调递减;当$1<k\leqslant2$时,$f^\prime(k)>0$,$f(k)$单调递增.
所以$f(k)_{\min}=f(1)=1^{2}+\frac{2}{1}=3$,即四边形$PNOM$面积的最小值为$3$.
(1)直线$l_{1}$的斜率$k_{1}=\frac{3 - 2}{-1 - 1}=-\frac{1}{2}$,因为$l_{1}\perp l_{2}$,所以直线$l_{2}$的斜率$k_{2}=2$,又直线$l_{2}$过点$P(1,2)$,所以直线$l_{2}$的方程为$y - 2 = 2(x - 1)$,即$2x - y = 0$.
(2)直线$l_{1}$的方程为$y - 2 = k(x - 1)$,令$x = 0$,得$y = 2 - k$,所以$N(0,2 - k)$;令$y = 0$,得$x = 1-\frac{2}{k}$,所以$T(1-\frac{2}{k},0)$.
直线$l_{2}$的斜率$k_{l_{2}}=\frac{2-( \frac{2}{k^{2}} + 2)}{1-0}=-\frac{2}{k^{2}}$,则直线$l_{2}$的方程为$y - 2 = -\frac{2}{k^{2}}(x - 1)$,令$y = 0$,得$x = k^{2}+1$,所以$M(k^{2}+1,0)$.
所以四边形$PNOM$的面积$S = S_{\triangle OPM}-S_{\triangle ONT}=\frac{1}{2}(k^{2}+1)\times2-\frac{1}{2}(1 - \frac{2}{k})(2 - k)=k^{2}+\frac{2}{k}$.
令$f(k)=k^{2}+\frac{2}{k}(0<k\leqslant2)$,则$f^\prime(k)=2k-\frac{2}{k^{2}}=\frac{2(k^{3}-1)}{k^{2}}$,令$f^\prime(k)=0$,得$k = 1$.
当$0<k<1$时,$f^\prime(k)<0$,$f(k)$单调递减;当$1<k\leqslant2$时,$f^\prime(k)>0$,$f(k)$单调递增.
所以$f(k)_{\min}=f(1)=1^{2}+\frac{2}{1}=3$,即四边形$PNOM$面积的最小值为$3$.
查看更多完整答案,请扫码查看


