《2025年练习生高中数学选择性必修第一册人教A版》

1. [2023·北京首师大附中通州校区高二月考]已知向量$\boldsymbol{a}=(1,1,0)$，则与$\boldsymbol{a}$同向共线的单位向量$\boldsymbol{e}=$( )
A. $(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2},0)$
B. $(0,1,0)$
C. $(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2},0)$
D. $(-1,-1,0)$

答案： C

2. [2022·四川成都蒲江中学高二月考]已知长方体$OABC - O_{1}A_{1}B_{1}C_{1}(O$为原点)中三顶点的坐标分别为$A(4,0,0)$，$C(0,3,0)$，$O_{1}(0,0,5)$，则此长方体外接球的球心坐标为( )
A. $(2,\frac{3}{2},\frac{5}{2})$
B. $(\frac{3}{2},2,\frac{5}{2})$
C. $(\frac{3}{2},4,\frac{5}{2})$
D. $(\frac{3}{2},2,5)$

答案： A

3. [2022·浙江杭州第二中学高二期中]已知$O$为空间任意一点，$A$，$B$，$C$，$P$满足任意三点不共线，但四点共面，且$\overrightarrow{BP}=m\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$，则$m$的值为( )
A. -1
B. 2
C. -2
D. -3

答案： C

4. [2023·山东临沂兰陵第四中学高二月考]已知向量$\boldsymbol{a}=(1,0,\sqrt{3})$，单位向量$\boldsymbol{b}$满足$|\boldsymbol{a}+2\boldsymbol{b}|=2\sqrt{3}$，则$\boldsymbol{a}$，$\boldsymbol{b}$的夹角为( )
A. $\frac{\pi}{6}$
B. $\frac{\pi}{4}$
C. $\frac{\pi}{3}$
D. $\frac{2\pi}{3}$

答案： C

5. [2022·四川绵阳南山中学高二期中]如图，$OABC$是四面体，$G$是$\triangle ABC$的重心，$G_{1}$是$OG$上一点，且$\overrightarrow{OG}=3\overrightarrow{OG_{1}}$，则( )

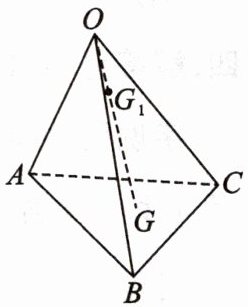
A. $\overrightarrow{OG_{1}}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$
B. $\overrightarrow{OG_{1}}=\frac{1}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$
C. $\overrightarrow{OG_{1}}=\frac{1}{4}\overrightarrow{OA}+\frac{1}{4}\overrightarrow{OB}+\frac{1}{4}\overrightarrow{OC}$
D. $\overrightarrow{OG_{1}}=\frac{1}{9}\overrightarrow{OA}+\frac{1}{9}\overrightarrow{OB}+\frac{1}{9}\overrightarrow{OC}$

答案： C

6. [2023·北京牛栏山一中高二月考]已知$\boldsymbol{a}$，$\boldsymbol{b}$，$\boldsymbol{c}$是不共面的三个向量，则下列各组向量中能构成空间的一个基底的是( )
A. $3\boldsymbol{a}$，$\boldsymbol{a}-\boldsymbol{b}$，$\boldsymbol{a}+2\boldsymbol{b}$
B. $2\boldsymbol{b}$，$\boldsymbol{b}-2\boldsymbol{a}$，$\boldsymbol{b}+2\boldsymbol{a}$
C. $\boldsymbol{a}$，$2\boldsymbol{b}$，$\boldsymbol{b}-\boldsymbol{c}$
D. $\boldsymbol{c}$，$\boldsymbol{a}+\boldsymbol{c}$，$\boldsymbol{a}-\boldsymbol{c}$

答案： C

7. [2023·贵州贵阳一中高二月考]如图，在四棱锥$P - ABCD$中，底面$ABCD$为正方形，$PA\perp$平面$ABCD$，$PA = AB$，$M$为$PC$上一动点，$PM = tPC$.若$\angle BMD$为钝角，则实数$t$的值不可能为( )

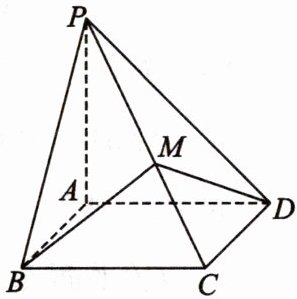
A. $\frac{1}{4}$
B. $\frac{1}{2}$
C. $\frac{2}{3}$
D. $\frac{3}{4}$

答案： B

8. [2022·广东江门广雅中学高二期中]如图，在棱长为1的正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，点$P$是$AA_{1}$的中点，点$M$，$N$是矩形$BB_{1}D_{1}D$内(包括边界)的任意两点，则$\overrightarrow{PM}\cdot\overrightarrow{PN}$的取值范围是( )

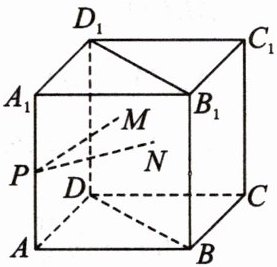
A. $[\frac{1}{4},\frac{5}{4}]$
B. $[-\frac{1}{4},\frac{5}{4}]$
C. $[\frac{1}{2},\frac{5}{4}]$
D. $[-\frac{1}{2},\frac{5}{4}]$

答案： B