《2025年练习生高中数学选择性必修第一册人教A版》

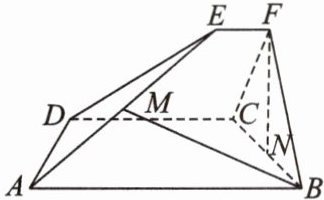
5. [2022·浙江高考]如图，已知ABCD和CDEF都是直角梯形，AB//DC，DC//EF，AB = 5，DC = 3，EF = 1，∠BAD = ∠CDE = 60°，二面角F - DC - B的平面角为60°.设M，N分别为AE，BC的中点.
(1)证明：FN⊥AD.
(2)求直线BM与平面ADE所成角的正弦值.

答案：

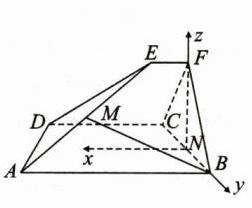
（1）【证明】由题意得 \(CD\perp BC\)，\(CD\perp FC\)，\(\therefore\angle FCB\) 即为二面角 \(F - CD - B\) 的平面角。\(\therefore\angle FCB = 60^{\circ}\)。由 \(BC\cap FC = C\)，得 \(CD\perp\) 平面 \(FCB\)。\(\because FN\subset\) 平面 \(FCB\)，\(\therefore CD\perp FN\)。易得 \(CF=\tan\angle CDE\cdot(CD - EF)=\sqrt{3}\times(3 - 1)=2\sqrt{3}\)，\(CB=\tan\angle BAD\cdot(AB - CD)=\sqrt{3}\times(5 - 3)=2\sqrt{3}\)，\(\therefore CF = CB\)。又 \(\because\angle FCB = 60^{\circ}\)，\(\therefore\triangle FBC\) 是等边三角形，\(\therefore CB\perp FN\)。又 \(\because CB\cap CD = C\)，\(\therefore FN\perp\) 平面 \(ABCD\)，\(\therefore FN\perp AD\)。 - （2）【解】\(\because FN\perp\) 平面 \(ABCD\)，\(\therefore\) 以点 \(N\) 为原点，过点 \(N\) 作与 \(CD\) 平行的直线，以该直线为 \(x\) 轴，以 \(NB,NF\) 所在直线分别为 \(y\) 轴、\(z\) 轴建立如图的空间直角坐标系，则 \(B(0,\sqrt{3},0)\)，\(A(5,\sqrt{3},0)\)，\(D(3,-\sqrt{3},0)\)，\(E(1,0,3)\)，\(M(3,\frac{\sqrt{3}}{2},\frac{3}{2})\)，\(\therefore\overrightarrow{BM}=(3,-\frac{\sqrt{3}}{2},\frac{3}{2})\)，\(\overrightarrow{DA}=(2,2\sqrt{3},0)\)，\(\overrightarrow{DE}=(-2,\sqrt{3},3)\)。设平面 \(ADE\) 的法向量为 \(\boldsymbol{m}=(x,y,z)\)，则 \(\begin{cases}\overrightarrow{DA}\cdot\boldsymbol{m}=0\\\overrightarrow{DE}\cdot\boldsymbol{m}=0\end{cases}\)，即 \(\begin{cases}2x + 2\sqrt{3}y = 0\\-2x+\sqrt{3}y + 3z = 0\end{cases}\)。取 \(x=\sqrt{3}\)，则 \(y=-1\)，\(z=\sqrt{3}\)，即 \(\boldsymbol{m}=(\sqrt{3},-1,\sqrt{3})\)。设 \(BM\) 与平面 \(ADE\) 所成的角为 \(\theta\)，则 \(\sin\theta=\frac{|\overrightarrow{BM}\cdot\boldsymbol{m}|}{|\overrightarrow{BM}||\boldsymbol{m}|}=\frac{|3\times\sqrt{3}+\frac{\sqrt{3}}{2}\times1+\frac{3}{2}\times\sqrt{3}|}{\sqrt{9+\frac{3}{4}+\frac{9}{4}}\times\sqrt{3 + 1+3}}=\frac{5\sqrt{7}}{14}\)。

6. [2021·北京高考]如图，在正方体ABCD - A₁B₁C₁D₁中，E为A₁D₁的中点，B₁C₁与平面CDE交于点F.
(1)求证：F为B₁C₁的中点.
(2)点M是棱A₁B₁上一点，且二面角M - FC - E的余弦值为√$\frac{5}{3}$，求A₁M/A₁B₁的值.

答案：
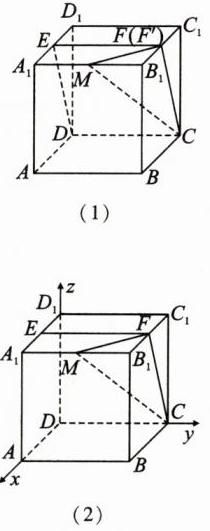
（1）【证明】如图（1），取 \(B_{1}C_{1}\) 的中点 \(F'\)，连接 \(EF',F'C\)。因为 \(ABCD - A_{1}B_{1}C_{1}D_{1}\) 为正方体，且 \(E,F'\) 分别为 \(A_{1}D_{1},B_{1}C_{1}\) 的中点，所以易得 \(EF'\parallel CD\)。所以 \(E,F',C,D\) 四点共面，所以平面 \(CDE\) 即为平面 \(CDEF'\)。所以直线 \(B_{1}C_{1}\) 交平面 \(CDE\) 于点 \(F'\)，所以点 \(F\) 与点 \(F'\) 重合，即点 \(F\) 为 \(B_{1}C_{1}\) 的中点。 - （2）【解】以点 \(D\) 为原点，\(DA,DC,DD_{1}\) 所在直线分别为 \(x\) 轴、\(y\) 轴、\(z\) 轴建立空间直角坐标系，如图（2）。不妨设正方体的棱长为 \(2\)，设 \(\frac{A_{1}M}{A_{1}B_{1}}=\lambda(0\leqslant\lambda\leqslant1)\)，则 \(M(2,2\lambda,2)\)，\(C(0,2,0)\)，\(F(1,2,2)\)，\(E(1,0,2)\)，所以 \(\overrightarrow{MC}=(-2,2 - 2\lambda,-2)\)，\(\overrightarrow{CF}=(1,0,2)\)，\(\overrightarrow{FE}=(0,-2,0)\)。设平面 \(MCF\) 的法向量为 \(\boldsymbol{m}=(x_{1},y_{1},z_{1})\)，则 \(\begin{cases}\boldsymbol{m}\cdot\overrightarrow{MC}=-2x_{1}+(2 - 2\lambda)y_{1}-2z_{1}=0\\\boldsymbol{m}\cdot\overrightarrow{CF}=x_{1}+2z_{1}=0\end{cases}\)。取 \(z_{1}=-1\)，得 \(x_{1}=2\)，\(y_{1}=\frac{1}{1-\lambda}\)，所以 \(\boldsymbol{m}=(2,\frac{1}{1-\lambda},-1)\)。设平面 \(CFE\) 的法向量为 \(\boldsymbol{n}=(x_{2},y_{2},z_{2})\)，则 \(\begin{cases}\boldsymbol{n}\cdot\overrightarrow{FE}=-2y_{2}=0\\\boldsymbol{n}\cdot\overrightarrow{CF}=x_{2}+2z_{2}=0\end{cases}\)。取 \(z_{2}=-1\)，得 \(x_{2}=2\)，\(y_{2}=0\)，所以 \(\boldsymbol{n}=(2,0,-1)\)。所以 \(\boldsymbol{m}\cdot\boldsymbol{n}=5\)，\(|\boldsymbol{m}|=\sqrt{5+(\frac{1}{1-\lambda})^{2}}\)，\(|\boldsymbol{n}|=\sqrt{5}\)，所以 \(\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle=\frac{\boldsymbol{m}\cdot\boldsymbol{n}}{|\boldsymbol{m}||\boldsymbol{n}|}=\frac{5}{\sqrt{5+(\frac{1}{1-\lambda})^{2}}\times\sqrt{5}}=\frac{\sqrt{5}}{3}\)，整理，得 \((1-\lambda)^{2}=\frac{1}{4}\)，解得 \(\lambda=\frac{1}{2}\) 或 \(\lambda=\frac{3}{2}\)（舍去）（需要注意 \(\lambda\) 的取值范围，舍去不符合题意的数值）。所以 \(\frac{A_{1}M}{A_{1}B_{1}}=\frac{1}{2}\)。

7. [2022·全国乙卷]如图，四面体ABCD中，AD⊥CD，AD = CD，∠ADB = ∠BDC，E为AC的中点.
(1)证明：平面BED⊥平面ACD.
(2)设AB = BD = 2，∠ACB = 60°，点F在BD上，当△AFC的面积最小时，求CF与平面ABD所成角的正弦值.

答案：

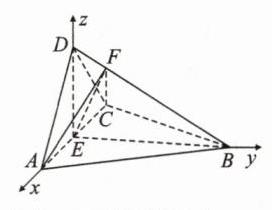
（1）【证明】\(\because AD = CD\)，\(\angle ADB=\angle BDC\)，\(BD = BD\)，\(\therefore\triangle ABD\cong\triangle CBD\)，\(\therefore AB = CB\)。\(\because E\) 为 \(AC\) 的中点，\(\therefore DE\perp AC\)，\(BE\perp AC\)。\(\because DE\cap BE = E\)，\(DE,BE\subset\) 平面 \(BED\)，\(\therefore AC\perp\) 平面 \(BED\)。\(\because AC\subset\) 平面 \(ACD\)，\(\therefore\) 平面 \(BED\perp\) 平面 \(ACD\)。 - （2）【解】如图，连接 \(EF\)。由（1）知 \(AC\perp\) 平面 \(BED\)。又 \(\because EF\subset\) 平面 \(BED\)，\(\therefore EF\perp AC\)。\(\therefore S_{\triangle AFC}=\frac{1}{2}AC\cdot EF\)。当 \(EF\perp BD\) 时，\(EF\) 的长最小，此时 \(\triangle AFC\) 的面积最小。由（1）知 \(AB = CB = 2\)。又 \(\because\angle ACB = 60^{\circ}\)，\(\therefore\triangle ABC\) 是边长为 \(2\) 的等边三角形，\(\therefore BE=\sqrt{3}\)。\(\because AD\perp CD\)，\(\therefore DE = 1\)，\(\therefore DE^{2}+BE^{2}=BD^{2}\)，\(\therefore DE\perp BE\)。以点 \(E\) 为原点，\(EA,EB,ED\) 所在直线分别为 \(x\) 轴、\(y\) 轴、\(z\) 轴建立空间直角坐标系，则 \(E(0,0,0)\)，\(A(1,0,0)\)，\(B(0,\sqrt{3},0)\)，\(C(-1,0,0)\)，\(D(0,0,1)\)，\(\therefore\overrightarrow{AB}=(-1,\sqrt{3},0)\)，\(\overrightarrow{AD}=(-1,0,1)\)，\(\overrightarrow{DB}=(0,\sqrt{3},-1)\)，\(\overrightarrow{ED}=(0,0,1)\)，\(\overrightarrow{EC}=(-1,0,0)\)。设 \(\overrightarrow{DF}=\lambda\overrightarrow{DB}(0\leqslant\lambda\leqslant1)\)，则 \(\overrightarrow{EF}=\overrightarrow{ED}+\overrightarrow{DF}=\overrightarrow{ED}+\lambda\overrightarrow{DB}=(0,0,1)+\lambda(0,\sqrt{3},-1)=(0,\sqrt{3}\lambda,1-\lambda)\)。\(\because EF\perp DB\)，\(\therefore\overrightarrow{EF}\cdot\overrightarrow{DB}=(0,\sqrt{3}\lambda,1-\lambda)\cdot(0,\sqrt{3},-1)=4\lambda-1 = 0\)，\(\therefore\lambda=\frac{1}{4}\)，\(\therefore\overrightarrow{EF}=(0,\frac{\sqrt{3}}{4},\frac{3}{4})\)，\(\therefore\overrightarrow{CF}=\overrightarrow{EF}-\overrightarrow{EC}=(0,\frac{\sqrt{3}}{4},\frac{3}{4})-(-1,0,0)=(1,\frac{\sqrt{3}}{4},\frac{3}{4})\)。设平面 \(ABD\) 的法向量为 \(\boldsymbol{n}=(x,y,z)\)，则 \(\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AB}=0\\\boldsymbol{n}\cdot\overrightarrow{AD}=0\end{cases}\)，即 \(\begin{cases}-x+\sqrt{3}y = 0\\-x + z = 0\end{cases}\)。取 \(y = 1\)，则 \(x=\sqrt{3}\)，\(z=\sqrt{3}\)，\(\therefore\boldsymbol{n}=(\sqrt{3},1,\sqrt{3})\)。设当 \(\triangle AFC\) 的面积最小时，\(CF\) 与平面 \(ABD\) 所成的角为 \(\theta\)，则 \(\sin\theta=|\cos\langle\boldsymbol{n},\overrightarrow{CF}\rangle|=\frac{|\boldsymbol{n}\cdot\overrightarrow{CF}|}{|\boldsymbol{n}||\overrightarrow{CF}|}=\frac{|\sqrt{3}\times1+1\times\frac{\sqrt{3}}{4}+\sqrt{3}\times\frac{3}{4}|}{\sqrt{3 + 1+3}\times\sqrt{1+\frac{3}{16}+\frac{9}{16}}}=\frac{4\sqrt{3}}{7}\)。故当 \(\triangle AFC\) 的面积最小时，\(CF\) 与平面 \(ABD\) 所成角的正弦值为 \(\frac{4\sqrt{3}}{7}\)。

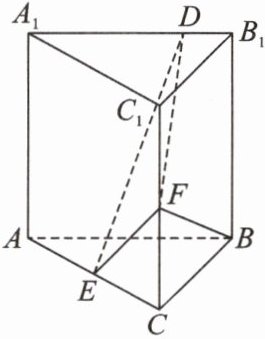
8. [2021·全国甲卷]已知直三棱柱ABC - A₁B₁C₁中，侧面AA₁B₁B为正方形，AB = BC = 2，E，F分别为AC和CC₁的中点，D为棱A₁B₁上的点，且BF⊥A₁B₁.
(1)证明：BF⊥DE.
(2)当B₁D为何值时，平面BB₁C₁C与平面DFE所成的二面角的正弦值最小？

答案：

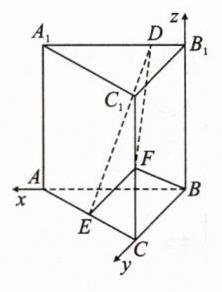
（1）【证明】 - **方法一**：因为三棱柱 \(ABC - A_{1}B_{1}C_{1}\) 是直三棱柱，所以 \(BB_{1}\perp\) 底面 \(ABC\)，所以 \(BB_{1}\perp AB\)。因为 \(A_{1}B_{1}\parallel AB\)，\(BF\perp A_{1}B_{1}\)，所以 \(BF\perp AB\)。又 \(BB_{1}\cap BF = B\)，\(BB_{1},BF\subset\) 平面 \(BCC_{1}B_{1}\)，所以 \(AB\perp\) 平面 \(BCC_{1}B_{1}\)。所以 \(BA,BC,BB_{1}\) 两两垂直。以 \(B\) 为原点，\(BA,BC,BB_{1}\) 所在直线分别为 \(x\) 轴、\(y\) 轴、\(z\) 轴建立空间直角坐标系，如图，则 \(B(0,0,0)\)，\(A(2,0,0)\)，\(E(1,1,0)\)，\(F(0,2,1)\)。所以 \(\overrightarrow{BF}=(0,2,1)\)。由题意，设 \(D(a,0,2)(0\leqslant a\leqslant2)\)，则 \(\overrightarrow{DE}=(1 - a,1,-2)\)，所以 \(\overrightarrow{BF}\cdot\overrightarrow{DE}=0\times(1 - a)+2\times1+1\times(-2)=0\)，所以 \(BF\perp DE\)。 - **方法二**：因为 \(BF\perp A_{1}B_{1}\)，所以 \(\overrightarrow{BF}\cdot\overrightarrow{A_{1}B_{1}}=0\)。又 \(A_{1}B_{1}\parallel AB\)，所以 \(BF\perp AB\)，所以 \(\overrightarrow{BF}\cdot\overrightarrow{AB}=0\)，所以 \(\overrightarrow{BF}\cdot\overrightarrow{ED}=\overrightarrow{BF}\cdot(\overrightarrow{EB}+\overrightarrow{BB_{1}}+\overrightarrow{B_{1}D})=\overrightarrow{BF}\cdot\overrightarrow{B_{1}D}+\overrightarrow{BF}\cdot(\overrightarrow{EB}+\overrightarrow{BB_{1}})=\overrightarrow{BF}\cdot\overrightarrow{EB}+\overrightarrow{BF}\cdot\overrightarrow{BB_{1}}=\overrightarrow{BF}\cdot(-\frac{1}{2}\overrightarrow{BA}-\frac{1}{2}\overrightarrow{BC})+\overrightarrow{BF}\cdot\overrightarrow{BB_{1}}=-\frac{1}{2}\overrightarrow{BF}\cdot\overrightarrow{BA}-\frac{1}{2}\overrightarrow{BF}\cdot\overrightarrow{BC}+\overrightarrow{BF}\cdot\overrightarrow{BB_{1}}=-\frac{1}{2}|\overrightarrow{BF}||\overrightarrow{BC}|\cos\angle FBC+|\overrightarrow{BF}||\overrightarrow{BB_{1}}|\cos\angle FBB_{1}=-\frac{1}{2}\times\sqrt{5}\times2\times\frac{2}{\sqrt{5}}+\sqrt{5}\times2\times\frac{1}{\sqrt{5}}=0\)，所以 \(BF\perp ED\)。 - （2）【解】由（1）可知 \(\overrightarrow{EF}=(-1,1,1)\)，\(\overrightarrow{DE}=(1 - a,1,-2)\)。设平面 \(DFE\) 的法向量为 \(\boldsymbol{m}=(x,y,z)\)，则 \(\begin{cases}\boldsymbol{m}\cdot\overrightarrow{EF}=0\\\boldsymbol{m}\cdot\overrightarrow{DE}=0\end{cases}\)，即 \(\begin{cases}-x + y+z = 0\\(1 - a)x + y-2z = 0\end{cases}\)。令 \(z = 2 - a\)，则 \(x = 3\)，\(y = 1 + a\)，所以 \(\boldsymbol{m}=(3,1 + a,2 - a)\)。易知平面 \(BCC_{1}B_{1}\) 的一个法向量为 \(\overrightarrow{BA}=(2,0,0)\)。设平面 \(BCC_{1}B_{1}\) 与平面 \(DEF\) 的二面角的平面角为 \(\theta\)，则 \(|\cos\theta|=\frac{|\boldsymbol{m}\cdot\overrightarrow{BA}|}{|\boldsymbol{m}||\overrightarrow{BA}|}=\frac{6}{\sqrt{2a^{2}-2a + 14}\times2}=\frac{3}{\sqrt{2a^{2}-2a + 14}}\)。当 \(a=\frac{1}{2}\) 时，\(2a^{2}-2a + 4\) 取得最小值，为 \(\frac{27}{2}\)，此时 \(\cos\theta\) 取得最大值，为 \(\frac{3}{\sqrt{\frac{27}{2}}}=\frac{\sqrt{6}}{3}\)。所以 \((\sin\theta)_{\min}=\sqrt{1 - (\frac{\sqrt{6}}{3})^{2}}=\frac{\sqrt{3}}{3}\)，此时 \(B_{1}D=\frac{1}{2}\)。 ### 方法总结 第一问，采用方法一，建立合适的空间直角坐标系，借助空间向量求解是最简单的方法，也是最优解；采用方法二，则是利用空间向量的加、减运算法则及数量积的定义运算进行证明，不是很常用的方法，不过这道题用这种方法过程也很简单，可以开拓思维。