《2025年练习生高中数学选择性必修第一册人教A版》

11. [2022·江西九江高二期中]过点 A(3,-1)且在两坐标轴上截距的绝对值相等的直线有（ ）
A. 2 条
B. 3 条
C. 4 条
D. 无数多条

答案： B

12. [2023·山东日照一中高二阶段练习]若一条光线从点$A(-\frac{1}{2},0)$处射到点 B(0,1)后被 y 轴反射，则反射光线所在直线的方程为（ ）
A. 2x - y - 1 = 0
B. 2x + y - 1 = 0
C. x - 2y - 1 = 0
D. x + 2y + 1 = 0

答案： B

13. 在△ABC 中，已知点 A(5,-2)，B(7,3)，且 AC 边的中点 M 在 y 轴上，BC 边的中点 N 在 x 轴上，则直线 MN 的方程为（ ）
A. 5x - 2y - 5 = 0
B. 2x - 5y - 5 = 0
C. 5x - 2y + 5 = 0
D. 2x - 5y + 5 = 0

答案： D

14. 甲同学在高考中，某选考科目成功进入 A 档. 那一年，全省该科目进入 A 档的考生们的卷面分最高为 92 分，最低为 85 分. 按规则将用一条“直线”对这些分数“折算”，其中 92 分“折算”为 100 分，85 分“折算”为 86 分. 若甲同学该科得分被“折算”为 96 分，则甲同学该科卷面分为（ ）
A. 89 分
B. 90 分
C. 91 分
D. 92 分

答案： B

15. 若直线 l 在 x 轴、y 轴上的截距的倒数之和为常数$\frac{1}{k}$，则该直线必过定点（ ）
A. (0,0)
B. (1,1)
C. (k,k)
D. $(\frac{1}{k},\frac{1}{k})$

答案： C

16. 已知经过第一、二、四象限的直线$l:\frac{x}{a}+\frac{y}{b}=1$经过点 P(2,1)，则 2a + b 的最小值为（ ）
A. 4
B. 4$\sqrt{2}$
C. 8
D. 9

答案： D

17. [2022·湖北鄂南高级中学高二阶段练习]过点(1,3)作直线 l，若 l 经过点(a,0)和(0,b)，且 a，b∈N*，则可作出的直线 l 的条数为（ ）
A. 1
B. 2
C. 3
D. 多于 3

答案： B

18. [2023·北京怀柔第一中学高二期中]已知直线 l 经过点 P(2,2)，O 为原点.
(1)若直线 l 过点 Q(-2,0)，求直线 l 的方程，并求直线 l 与两坐标轴围成的三角形的面积；
(2)如果直线 l 在两坐标轴上的截距之和为 8，求直线 l 的方程.

答案：
(1)直线$l$的斜率$k=\frac{2 - 0}{2-(-2)}=\frac{1}{2}$，由点斜式得直线$l$方程为$y-0=\frac{1}{2}(x + 2)$，即$x - 2y+2 = 0$。令$x = 0$，得$y = 1$；令$y = 0$，得$x=-2$。所以直线$l$与两坐标轴围成的三角形面积$S=\frac{1}{2}\times| - 2|\times1 = 1$。
(2)设直线$l$方程为$\frac{x}{a}+\frac{y}{b}=1$，则$\begin{cases}a + b = 8\\\frac{2}{a}+\frac{2}{b}=1\end{cases}$，由$a + b = 8$得$b = 8 - a$，代入$\frac{2}{a}+\frac{2}{b}=1$得$\frac{2}{a}+\frac{2}{8 - a}=1$，化简得$a^{2}-8a + 16 = 0$，解得$a = 4$，$b = 4$或$a = 2$，$b = 6$或$a = 6$，$b = 2$。所以直线$l$的方程为$x + y - 4 = 0$或$3x + y - 6 = 0$或$x+3y - 6 = 0$。

19. 为了绿化城市，拟在如图所示的矩形区域 ABCD 内建一个矩形草坪 PQCR(P 在线段 EF 上)，其中在△AEF 区域内有一文物保护区不能被占用. 经测量 AB = 100 m，BC = 80 m，AE = 30 m，AF = 20 m，当$\frac{EP}{PF}$为何值时才能使草坪面积最大？求出草坪的最大面积.

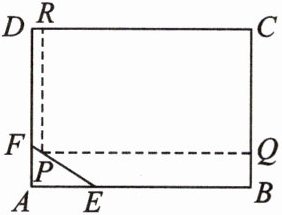
答案： 以$A$为原点，分别以$AB$，$AD$所在直线为$x$轴，$y$轴建立平面直角坐标系。则$E(30,0)$，$F(0,20)$，直线$EF$的方程为$\frac{x}{30}+\frac{y}{20}=1$，设$P(x,y)$，则$y = 20-\frac{2}{3}x$。矩形草坪$PQCR$的面积$S=(100 - x)(80 - y)=(100 - x)[80-(20-\frac{2}{3}x)]=(100 - x)(60+\frac{2}{3}x)=-\frac{2}{3}x^{2}+\frac{20}{3}x + 6000=-\frac{2}{3}(x - 5)^{2}+6000+\frac{50}{3}$。当$x = 5$时，$y=\frac{50}{3}$，$\frac{EP}{PF}=\frac{\sqrt{(5 - 30)^{2}+(\frac{50}{3}-0)^{2}}}{\sqrt{(5 - 0)^{2}+(\frac{50}{3}-20)^{2}}}=5$，$S_{max}=6000+\frac{50}{3}=\frac{18050}{3}(m^{2})$。所以当$\frac{EP}{PF}=5$时，草坪面积最大，最大面积为$\frac{18050}{3}m^{2}$。